Вычисление абсолютной погрешности является важным навыком в математике и статистике. Он используется для количественной оценки разницы между фактическим значением измерения или расчета и предполагаемым или прогнозируемым значением. Абсолютная погрешность служит мерой точности и часто используется в различных научных и инженерных дисциплинах.
Для расчета абсолютной погрешности необходимы два значения: фактическое или истинное значение и расчетное или прогнозируемое значение. Абсолютная погрешность получается путем взятия абсолютной разницы между этими двумя значениями. Это гарантирует, что ошибка всегда положительна, независимо от того, больше или меньше расчетное значение фактического.
Абсолютная ошибка - это простая и полезная концепция, поскольку она позволяет оценить точность расчета или измерения. Это особенно важно при работе с чувствительными или критическими данными, где даже небольшие ошибки могут иметь серьезные последствия. Вычисляя абсолютную погрешность, можно определить отклонения от истинного значения и внести необходимые коррективы для повышения точности результата.
Помимо расчета абсолютной погрешности отдельного измерения или вычисления, его можно использовать для сравнения точности различных методов или моделей. Рассчитав абсолютную погрешность каждого метода или модели, можно определить, какой из них обеспечивает наиболее точные результаты. Такой сравнительный анализ позволяет выбрать наиболее надежный метод или модель для конкретных нужд.
В целом, расчет абсолютной погрешности - это фундаментальный навык, широко используемый в математике, статистике и различных научных и инженерных дисциплинах. Он помогает количественно оценить точность измерений и вычислений и позволяет сравнивать различные методы и модели. Овладение навыком расчета абсолютной погрешности обеспечивает обоснованность и надежность результатов и способствует прогрессу в данной области.
Что такое абсолютная погрешность?
Абсолютная погрешность - это математический термин, используемый для количественной оценки разницы между расчетным или измеренным значением и истинным или ожидаемым значением. Он описывает величину отклонения, независимо от того, является ли отклонение положительным или отрицательным. Абсолютная погрешность часто используется для оценки точности измерения или расчета.
При расчете абсолютной погрешности расчетное или измеренное значение вычитается из истинного или ожидаемого значения. Полученная разница является абсолютной погрешностью. Она представляет собой число, показывающее, насколько оценка или измерение далеки от истинного значения.
Абсолютная погрешность может быть выражена с использованием различных единиц, в зависимости от обстоятельств измерения или расчета. Например, если длина объекта измеряется в сантиметрах, абсолютная погрешность выражается в сантиметрах. Единицы абсолютной погрешности должны соответствовать единицам измерения или вычисления.
Абсолютная погрешность обычно выражается в виде положительного значения. Это облегчает сравнение и интерпретацию точности различных измерений или вычислений. Абсолютная погрешность также может быть использована для определения процентной погрешности путем деления абсолютной погрешности на истинное значение и умножения на 100.
Определение абсолютной погрешности и ее значение в расчетах
Понятие абсолютной погрешности является фундаментальным понятием в области математики и статистики. Она означает разницу между измеренным или наблюдаемым значением и истинным или ожидаемым значением. Абсолютная погрешность - это способ количественной оценки того, насколько близко или точно измерение или расчеты соответствуют действительному значению. Обычно она выражается в виде положительной величины.
Абсолютная погрешность играет важную роль в различных расчетах и анализах. Она позволяет оценить качество и надежность измерений, прогнозов и математических моделей. Вычисление абсолютной погрешности позволяет оценить точность и прецизионность расчетов, выявить потенциальные источники погрешности и принять обоснованные решения и корректировки.
Чтобы рассчитать абсолютную погрешность, вычтите истинное значение из измеренного, получите абсолютное значение результата и выразите его в соответствующих единицах. Например, если вы измеряете длину объекта и фактическая длина равна 10 сантиметрам, а измеренная - 9,5 сантиметра, абсолютная погрешность составляет 0,5 сантиметра.
Важно отметить, что абсолютная погрешность отличается от относительной погрешности. Абсолютная погрешность представляет собой абсолютную меру того, насколько измерение или расчеты далеки от истинного значения, в то время как относительная погрешность выражает абсолютную погрешность в виде доли или процента от истинного значения. И абсолютная, и относительная погрешности являются ценными инструментами для оценки точности и аккуратности вычислений.
Как рассчитать абсолютную погрешность
Чтобы рассчитать абсолютную погрешность, выполните следующие действия
Определите истинное значение: это правильное или точное значение, которое необходимо сравнить с измеренным или рассчитанным значением. Обычно оно дано или известно заранее.
Получение измеренного или рассчитанного значения: это значение, полученное в результате измерения или расчета. Оно не совпадает с истинным значением и может содержать некоторые ошибки.
Вычислить абсолютную разность: вычесть истинное значение из измеренного или рассчитанного значения. Абсолютная разность - это величина расхождения между двумя значениями, независимо от направления.
Формула абсолютной погрешности: вычислите абсолютную погрешность по формуле: абсолютная погрешность = | истинное значение - измеренное значение|.
Абсолютная погрешность выражает, насколько далеко измерение или вычисление от истинного значения, без учета направления. Она представляет собой количественную меру расхождения между двумя значениями.
Важно отметить, что абсолютная погрешность не всегда отрицательна, поскольку она представляет собой величину ошибки. Кроме того, поскольку абсолютная ошибка не дает информации о направлении ошибки, она часто используется в сочетании с другими измерениями, такими как относительная ошибка или процентная ошибка, чтобы обеспечить более полное понимание точности измерения или ошибки. Расчет.
Расчет абсолютной погрешности позволяет оценить уровень точности измерения или расчета, определить источники погрешности и внести необходимые коррективы для улучшения общего качества результатов.
Пошаговое руководство и примеры расчета абсолютной погрешности
Вычисление абсолютной погрешности - важный математический и научный навык. Он позволяет определить величину разницы между расчетным или измеренным значением и истинным или допустимым значением. Ниже приводится пошаговое руководство по расчету абсолютной погрешности.
Шаг 1: Определите истинное или допустимое значение. Это то значение, которое считается наиболее точным или правильным.
Шаг 2: Измерьте или оцените интересующую вас величину. Это может быть длина, вес, температура или другая величина.
Шаг 3: Вычтите истинное значение из измеренного или оцененного значения. Это дает разницу между двумя значениями.
Шаг 4: Получите абсолютное значение разности, рассчитанной на шаге 3. Это важно, поскольку абсолютная погрешность всегда должна быть положительной, независимо от того, больше или меньше истинного значения измеренное значение.
Шаг 5: Округлите абсолютную погрешность до соответствующих значащих цифр. Это зависит от точности измерения или оценки.
Давайте рассмотрим пример, иллюстрирующий расчет абсолютной погрешности. Предположим, вы измеряете длину палки, длина которой, как известно, составляет ровно 10 сантиметров. Результат измерения - 10,3 сантиметра. Вот как можно рассчитать абсолютную погрешность
Истинное значение: 10 сантиметров
Фактическое значение: 10,3 сантиметра
Разница: 10. 3 - 10 = 0. 3 сантиметра
Абсолютное значение: |0. 3|= 0. 3 сантиметра
Таким образом, в данном примере абсолютная ошибка составляет 0. 3 сантиметра.
Обратите внимание, что абсолютная погрешность представляет собой величину разницы между измеренным или оцененным значением и истинным или допустимым значением. Это важное понятие для понимания и точного расчета в различных научных и математических приложениях.

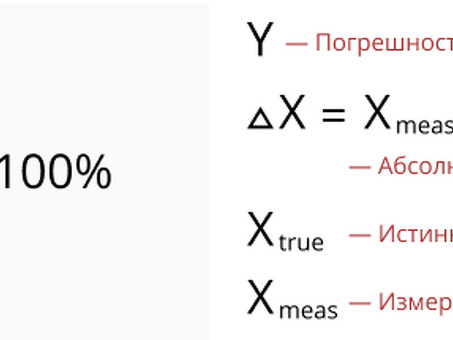



Комментарии