Автоматический расчет t-теста Стьюдента

t-тест Стьюдента - это статистический тест, обычно используемый для определения наличия существенной разницы между средними значениями двух групп. Он широко используется в различных областях, включая медицину, экономику и социальные науки. Ручной расчет t-тестов может быть утомительным и трудоемким процессом. Однако благодаря технологическому прогрессу этот процесс теперь можно автоматизировать и получить результаты t-теста всего за несколько кликов. Существуют различные программы и языки программирования, которые могут автоматически рассчитывать t-тесты Стьюдента. Эти инструменты не только экономят время и усилия, но и обеспечивают точность вычислений. Они обеспечивают простой и прямой способ ввода данных и генерации тестовой статистики и p-значений. Автоматический калькулятор t-тестов может работать с различными типами t-тестов, включая независимые выборочные t-тесты, парные выборочные t-тесты и одновыборочные t-тесты. Он также настраивается, позволяя пользователю указать желаемый уровень значимости и доверительный интервал. Что такое t-тест Стьюдента? t-тест Стьюдента - это статистический тест, используемый для определения наличия существенной разницы между средними значениями двух групп. Он назван в честь его создателя Уильяма Сили Госсета, который опубликовал метод под псевдонимом "Стьюдент" в 1908 году. Тест часто используется при проверке гипотез, когда среднее значение выборки сравнивается с известным или предполагаемым средним значением популяции. Он особенно полезен, когда размер выборки мал или когда неизвестно стандартное отклонение популяции. В t-тесте рассчитывается t-значение, которое представляет собой разницу между средними двух групп для внутригрупповой вариации; чем выше t-значение, тем больше вероятность того, что разница между двумя средними статистически значима. Существуют различные типы t-тестов, включая t-тест двух независимых выборок, t-тест парных выборок и t-тест одной выборки. Независимый двухвыборочный t-тест используется для сравнения средних двух независимых групп, например, тестовых оценок мальчиков и девочек. Т-тест парных выборок используется, когда индивидуумы из одной группы измеряются в два разных момента времени или при двух разных условиях; t-тест одной выборки используется для сравнения среднего значения выборки со средним значением известной популяции. t-тест основывается на определенных предположениях, например, что данные нормально распределены или что вариации двух групп равны. Если эти предположения нарушаются, это может повлиять на достоверность результатов t-теста. Кроме того, t-тест предполагает, что наблюдения в каждой группе независимы, а выборка случайна. В заключение следует отметить, что t-тест Стьюдента - это широко используемый статистический тест для сравнения средних двух групп. Он позволяет определить, является ли разница между наблюдаемыми средними значительной или просто случайной. Почему t-тест Стьюдента важен? t-тест Стьюдента - это важный статистический инструмент, используемый для определения того, существует ли значительная разница между средними двух групп. Он был разработан Уильямом Сили Госсетом. Он публиковался под псевдонимом "Студент" из-за ограничений компании на публикацию его исследований. t-тесты широко используются в различных областях, включая психологию, медицину, экономику и социальные науки. Одна из основных причин важности t-теста Стьюдента заключается в том, что он позволяет исследователям делать выводы о параметрах популяции на основе выборочных данных: сравнивая средние значения двух групп, исследователи могут оценить, являются ли наблюдаемые различия статистически значимыми или просто случайными. t-тест используется для определения разницы между средними значениями двух групп. t-тест также ценен тем, что учитывает вариации внутри каждой группы и размер выборки, что делает его более надежным, чем другие тесты, такие как z-тест. Он подходит для ситуаций, когда размер выборки мал или когда неизвестно стандартное отклонение популяции. t-тест Стьюдента часто используется при проверке гипотез, когда исследователь формулирует нулевую гипотезу (нет различий между двумя группами) и альтернативную гипотезу (есть различия между двумя группами). Выполнив t-тест и рассчитав p-значение, исследователь может определить, следует ли отвергнуть нулевую гипотезу. Кроме того, t-тесты позволяют исследователям сравнивать различные переменные или условия в рамках одной группы. Например, его можно использовать для оценки того, есть ли значительные различия в результатах тестов до и после вмешательства, или есть ли различия в уровнях кровяного давления у мужчин и женщин. В целом, t-тест Стьюдента - это мощный и широко используемый статистический инструмент, который помогает исследователям принимать обоснованные решения на основе выборочных данных. Его гибкость и способность работать с небольшими объемами выборки сделали его важной частью методологии исследований во многих областях. Вычисление t-теста Стьюдента t-тест Стьюдента - это статистический тест, используемый для определения наличия существенной разницы между средними значениями двух групп. Он был разработан Уильямом Сили Госсетом, который опубликовал его под псевдонимом "Студент" из-за ограничений на публикацию, наложенных его работодателем. Для расчета t-теста Стьюдента вам понадобятся среднее значение, стандартное отклонение и размер выборки для двух сравниваемых групп. Сначала вычисляется разница между двумя средними. Это числитель формулы t-теста. Затем вычислите стандартное отклонение. Это квадратный корень из суммы квадратов стандартных отклонений, деленный на сумму объемов выборки. Это знаменатель уравнения t-теста. Затем разница между средними делится на стандартную ошибку. Это дает t-значение, которое определяет, насколько разница между средними отличается от нуля на стандартную ошибку; более высокое t-значение указывает на большую разницу между средними. 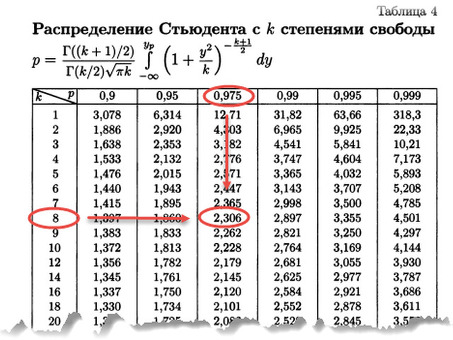Наконец, t-значение можно сравнить с критическим значением в таблице t-распределения (на основе степеней свободы и требуемого уровня значимости); если t-значение больше критического значения, можно сделать вывод, что между средними двух групп существует значительная разница. В качестве альтернативы можно использовать статистическое программное обеспечение или онлайн-калькуляторы для автоматического расчета t-значения и определения значимости разницы между средними. Эти инструменты часто предоставляют дополнительную информацию, такую как степени свободы, p-значения и доверительные интервалы. t-тест Стьюдента широко используется в различных областях, включая психологию, биологию и экономику. Это мощный инструмент для сравнения двух групп и определения того, есть ли между ними значимые различия. Формула t-теста Стьюдента t-тест Стьюдента - это статистический тест, используемый для определения наличия значимой разницы между средними значениями двух групп. Он часто используется при проверке гипотез и основан на t-распределении - математическом распределении, представляющем связь между средним значением выборки и популяции в целом. Формула для t-теста Стьюдента зависит от различных факторов, таких как размер выборки, среднее и стандартное отклонение двух сравниваемых групп. t-тесты бывают двух основных типов: независимый выборочный t-тест, который сравнивает средние двух независимых групп, и заочный выборочный t-тест, который сравнивает средние двух связанных групп. Второй тип - это t-тест выборки соответствия, в котором сравниваются средства двух связанных групп. Формула для независимого выборочного t-теста следующая t = (x1 - x2) / sqrt((s1^2 / n1) + (s2^2 / n2)) где t - t-значение, x1 и x2 - средние значения двух групп, s1 и s2 - стандартные отклонения двух групп, а n1 и n2 - объемы выборки двух групп. В случае парного выборочного t-теста формула немного отличается t = (x̄d - μd) / (sd / √n) где t - t-значение, x̄d - средняя разница между парными наблюдениями, µd - материнская средняя разница (обычно принимается равной нулю), sd - стандартное отклонение разницы, а n - количество пар. Используя эти уравнения, исследователи могут рассчитать t-значение, которое может быть использовано для определения вероятности случайного наблюдения разницы между двумя группами. Если рассчитанное t-значение достаточно велико, это говорит о том, что разница между двумя группами вряд ли обусловлена случайной вариацией и может считаться статистически значимой. Процесс пошагового расчета Расчет t-теста Стьюдента включает в себя несколько шагов для определения статистической значимости разницы между двумя группами. Вкратце этот процесс можно описать следующим образом. Определите нулевую гипотезу. Начните с формулировки нулевой гипотезы. Нулевая гипотеза предполагает, что между средними значениями двух сравниваемых групп нет существенной разницы. Собрать данные: собрать данные от двух сравниваемых групп и убедиться, что данные репрезентативны и несмещены. Вычислить среднее значение: определить среднее значение для каждой группы путем суммирования всех значений и деления на общее количество наблюдений в каждой группе. Вычислите стандартное отклонение: вычислите стандартное отклонение для каждой группы. Это измеряет вариацию или разброс данных внутри каждой группы. Вычислить стандартную ошибку: вычислить стандартную ошибку для каждой группы. Она представляет собой стандартное отклонение, деленное на квадратный корень из объема выборки. Вычислить t-значение: вычисляет t-значение по формуле Это измеряет, насколько отличаются средние значения двух групп по сравнению с вариацией внутри каждой группы. Определить степени свободы: вычислить степени свободы, которые представляют собой количество независимых наблюдений, которые могут быть использованы в тесте. Найти критическое t-значение: сравнить рассчитанное t-значение с критическим t-значением в таблице t-распределения, исходя из выбранного уровня значимости и степеней свободы. Интерпретируйте результаты: если рассчитанное t-значение больше критического t-значения, отвергните нулевую гипотезу и сделайте вывод о наличии значительной разницы между средними двух групп. В противном случае нулевая гипотеза не может быть отвергнута. Следуя этим процедурам, исследователи могут определить, являются ли различия, наблюдаемые между двумя группами, статистически значимыми, что дает ценное представление об эффективности исследуемого вмешательства или лечения.