При манипулировании данными или проведении измерений важно понимать понятие погрешности. Погрешность - это разница между измеренным и истинным значением величины. Обычно обсуждаются два типа погрешности: абсолютная погрешность и относительная погрешность.
Абсолютная погрешность определяется как разница между измеренным и истинным значением. Она указывает на степень отклонения измеренного значения от истинного. Абсолютная погрешность дает абсолютные величины, но не дает информации о величине погрешности по сравнению с истинным значением.
Относительная погрешность, с другой стороны, представляет собой способ выражения погрешности в процентах или соотношении. Она рассчитывается путем деления абсолютной ошибки на истинное значение и умножения на 100%. Относительная погрешность дает более четкое представление о точности измерения, поскольку абсолютную погрешность можно сравнить с истинным значением. Это особенно полезно при работе с величинами разной величины.
Благодаря технологическому прогрессу появились онлайн-инструменты для расчета абсолютной и относительной погрешности. Эти инструменты позволяют легко выполнять сложные расчеты и получать точные результаты. Будь вы студент, исследователь или эксперт, наличие доступа к онлайн-ресурсам значительно упрощает вашу работу и повышает точность измерений.
В заключение следует отметить, что при манипулировании данными или выполнении измерений важно понимать и рассчитывать абсолютные и относительные погрешности. С помощью онлайн-инструментов теперь легче, чем когда-либо, точно рассчитать этот тип погрешности и повысить точность вашей работы.
Понимание абсолютных и относительных погрешностей
Когда речь идет об измерении и вычислении погрешностей, обычно используются две метрики: абсолютная погрешность и относительная погрешность. Обе эти метрики помогают понять точность и аккуратность измерения или вычисления в различных ситуациях.
Абсолютная погрешность измеряет разницу между измеренным или рассчитанным значением и истинным или ожидаемым значением. Она представляет собой число, отражающее величину ошибки без учета величины или масштаба исходного значения. Абсолютная погрешность является важной метрикой в различных областях, где требуются точные измерения и вычисления, например, в физике, технике и статистике.
Относительная погрешность, с другой стороны, обеспечивает более контекстуальное понимание точности и аккуратности. Она рассчитывается путем деления абсолютной ошибки на истинное или ожидаемое значение и выражения результата в процентах путем умножения на 100. Это позволяет сравнивать точность различных измерений или вычислений, даже если они имеют разную величину. Относительная погрешность особенно полезна при сравнении наборов данных или оценке эффективности моделей или алгоритмов.
Например, предположим, вы измеряете длину объекта с помощью двух разных приборов. Абсолютная погрешность дает разницу между каждым измерением и фактической длиной объекта. Однако если точность одного прибора составляет 0,1 см, а точность другого - 0,01 см, то относительная погрешность помогает определить, какой прибор обеспечивает более точное измерение. Рассматривая относительную погрешность, можно учитывать как абсолютную разницу между приборами, так и их точность.
Важно отметить, что как абсолютная, так и относительная погрешность имеют ограничения и должны использоваться надлежащим образом в зависимости от контекста. Абсолютная погрешность может не отражать относительную точность, а относительная погрешность не всегда обеспечивает значимое сравнение, когда истинное значение близко к нулю. Поэтому при оценке погрешностей необходимо учитывать конкретные требования и ограничения каждой ситуации.
Определения и пояснения
Абсолютная ошибка и относительная ошибка - это два метода, используемые для измерения точности и погрешности числа по сравнению с его истинным или ожидаемым значением. Эти понятия широко используются в научных и математических расчетах.
Абсолютная погрешность: также известная как абсолютная разница, абсолютная погрешность - это разница между измеренным или приблизительным значением и истинным или ожидаемым значением. Она представляет собой величину ошибки, присутствующей в измерении. Абсолютная погрешность всегда выражается в тех же единицах, что и измеряемое значение.
Относительная погрешность: также известная как относительная разница, относительная погрешность - это абсолютная погрешность, деленная на истинное или ожидаемое значение. Она обеспечивает стандартизированный способ сравнения точности различных измерений или вычислений. Относительная погрешность обычно выражается в процентах или долях.
При оценке качества измерений и вычислений важны как абсолютные, так и относительные погрешности. Абсолютная ошибка дает числовое значение, отражающее размер ошибки, а относительная ошибка дает меру относительной точности, которая может быть использована для сравнения различных значений. Важно отметить, что как абсолютная, так и относительная погрешности должны быть как можно меньше, чтобы обеспечить надежность и достоверность данных или вычислений.
Чтобы рассчитать абсолютную погрешность, вычтите измеренное значение из истинного. Чтобы рассчитать относительную погрешность, разделите абсолютную погрешность на истинное значение. Обычно принято умножать относительную погрешность на 100, чтобы получить значение в процентах. Однако при расчете как абсолютной, так и относительной погрешности важно обеспечить соответствие единиц измерения.
Различия и применение
Абсолютная погрешность и относительная погрешность - это два разных способа измерения точности вычисленного значения по сравнению с истинным значением. Абсолютная погрешность представляет собой разницу между рассчитанным значением и истинным значением без учета масштаба или величины значения. Это полезная мера, когда величина ошибки имеет значение.
Относительная погрешность, с другой стороны, учитывает величину и масштаб соответствующих значений. Она рассчитывается путем деления абсолютной ошибки на истинное значение и выражается в процентах или долях. Относительная погрешность полезна при сравнении величин разного масштаба, так как она обеспечивает меру точности относительно размера истинного значения.
Как абсолютная, так и относительная погрешность могут использоваться для различных целей в разных областях. В научных исследованиях и экспериментах обе шкалы используются для оценки точности измерений и вычислений. Абсолютная погрешность помогает определить величину ошибки, а относительная погрешность дает представление о соотношении ошибки и истинного значения.
В таких областях, как финансы и экономика, относительная погрешность часто используется для оценки точности экономических прогнозов и предсказаний. Сравнивая относительные ошибки различных моделей и методов, аналитики могут определить, какой подход лучше с точки зрения точности и достоверности.
В производстве и машиностроении для оценки качества продукции и процессов часто используются абсолютные и относительные погрешности. Абсолютная погрешность помогает выявить отклонения от желаемых значений, а относительная погрешность дает представление о проценте погрешности относительно спецификации. Эта информация может быть использована для улучшения производственного процесса и обеспечения большего контроля качества.
В заключение следует отметить, что как абсолютная, так и относительная погрешность являются ценными мерами точности в различных ситуациях. Абсолютная погрешность фокусируется на величине ошибки, в то время как относительная погрешность учитывает масштаб значения. Понимание различий и применения этих измерений может помочь повысить точность измерений и улучшить процесс принятия решений в различных областях.
Вычисление абсолютной и относительной погрешности
При работе с измерениями и научными данными важно иметь возможность количественно оценить точность результатов. Здесь важны абсолютная и относительная погрешность. Абсолютная и относительная погрешности - это математические величины, с помощью которых данные можно сравнить с известными или ожидаемыми значениями.
Абсолютная погрешность - это мера того, насколько измеренное значение отличается от известного или ожидаемого значения. Она рассчитывается путем вычитания известного или ожидаемого значения из измеренного значения и получения абсолютного значения разницы. Например, если длина объекта измерена как 10,5 см, а фактическая длина составляет 10 см, абсолютная погрешность будет равна |10,5 - 10| = 0. 5 см.
Относительная погрешность, с другой стороны, учитывает величину измеренного значения. Она рассчитывается путем деления абсолютной погрешности на известное или ожидаемое значение и умножения на 100 для получения процента. Например, если абсолютная ошибка составляет 0,5 см, а известное или ожидаемое значение - 10 см, относительная ошибка равна (0,5/10) * 100 = 5%.
Как абсолютные, так и относительные погрешности полезны в разных ситуациях. Абсолютная погрешность дает возможность непосредственно измерить, насколько измеренное значение отличается от известного или ожидаемого, независимо от величины этого значения. Относительная погрешность, с другой стороны, может быть использована для сравнения точности измерений разной величины. Она часто используется при сравнении небольших изменений от ожидаемого значения.
При использовании абсолютных и относительных погрешностей важно отметить, что они являются инструментами для количественной оценки точности измерений и данных. Они не дают информации о причинах ошибок или качестве методики измерения. Всегда важно учитывать другие факторы, которые могут повлиять на точность результатов, такие как точность оборудования и техника измерения.
Формулы и процедуры расчета
Существуют специальные формулы и процедуры расчета, которые необходимо соблюдать для расчета абсолютных и относительных погрешностей. Эти расчеты позволяют сравнить точность измеренного или оцененного значения с известными или принятыми значениями.
Формула для абсолютной погрешности определяется как абсолютное значение разницы между измеренным или оцененным значением и известным или принятым значением. Математически это можно выразить следующим образом.
Абсолютная погрешность = | измеренное значение - принятое значение|
Для расчета относительной погрешности абсолютная погрешность делится на известное или принятое значение. Это обычно выражается в процентах для определения точности измерения или оценки. Математическое выражение для относительной погрешности следующее
Относительная погрешность = (абсолютная погрешность / принятое значение) * 100
Процедура расчета для нахождения абсолютной и относительной погрешности выглядит следующим образом
Определите измеряемое или оцениваемое значение и известное или принятое значение.
Вычтите известное или принятое значение из измеренного или оцененного значения, чтобы найти абсолютную разность.
Получите абсолютное значение разности, полученной на предыдущем этапе, чтобы исключить отрицательные показания.
Разделите абсолютную разницу на известное или принятое значение, чтобы найти относительную погрешность.
Умножьте относительную погрешность на 100 и выразите ее в процентах.
Этот процесс расчета позволяет количественно оценить точность измерения или оценки путем сравнения измеренного или оцененного значения с известным или принятым значением. Вычисляя абсолютную и относительную погрешность, можно оценить уровень точности, понимая, насколько измеренное или оцененное значение отклоняется от известного или принятого значения.
Примеры абсолютной и относительной погрешности
Когда речь идет об измерении погрешности, абсолютная и относительная погрешность являются двумя важными метриками. Давайте рассмотрим несколько примеров того, как можно рассчитать и интерпретировать эти погрешности.
Пример 1: Предположим, вы измеряете длину куска струны с помощью линейки. Фактическая длина струны составляет 10 см. Вы измеряете и обнаруживаете, что длина линейки составляет 9,7 см. Чтобы рассчитать абсолютную погрешность, вычтите истинное значение из измеренного. abs_error = |9. 7 - 10|= 0. 3 см. Относительную погрешность можно получить, разделив абсолютную погрешность на истинное значение: rel_error = (0. 3/10) * 100% = 3%.
Пример 2: Предположим, вы проводите эксперимент по определению ускорения под действием силы тяжести. Допустимое значение составляет 9,8 м/с². Вы проводите эксперимент и получаете значение 9,5 м/с². Абсолютная ошибка рассчитывается как abs_error = |9.5 - 9.8|. = 0. 3 м/с². Относительная ошибка находится путем деления абсолютной ошибки на допуск: rel_error = (0. 3/9. 8) * 100% = 3. 06%.
Пример 3: Рассмотрим сценарий вычисления площади прямоугольника. Фактическая площадь составляет 50 квадратных единиц. Однако из-за ошибки в вычислениях получена площадь 53 квадратных единицы. Абсолютная ошибка равна abs_error = |53 - 50|. = 3 квадратных единицы. Относительная ошибка - rel_error = (3/50) * 100% = 6%.
Пример 4: Представьте, что вы оцениваете численность населения города. Истинное население составляет 1 миллион человек, но вы оцениваете его в 900 000. Абсолютная ошибка рассчитывается как abs_error = |900, 000 - 1, 000, 000|. = 100 000 человек. Относительная ошибка - rel_error = (100, 000/1, 000, 000) * 100% = 10%.
Эти примеры показывают, как абсолютная и относительная погрешность могут помочь в оценке точности и аккуратности измерений и вычислений. Абсолютная погрешность непосредственно измеряет разницу между измеренным и истинным значением, а относительная погрешность обеспечивает стандартизированный метод сравнения погрешностей между различными измеренными или вычисленными значениями.
Сценарии реального мира
В реальных сценариях понимание и расчет абсолютных и относительных погрешностей может быть очень полезным для различных целей. Одно из распространенных применений - инженерная сфера, где точность и аккуратность имеют решающее значение. Например, при проектировании и испытании мостов инженерам необходимо обеспечить максимальную точность измерений и расчетов. Вычисляя абсолютные и относительные погрешности, можно определить степень точности и внести необходимые коррективы для улучшения конструкции.
Еще один реальный сценарий, в котором встречаются абсолютные и относительные ошибки, - это прогнозирование погоды. Метеорологи полагаются на данные из различных источников для точного прогнозирования погодных условий. Однако из-за сложности, присущей погодным системам, в этих прогнозах всегда присутствует некоторая степень неопределенности. Рассчитывая абсолютные и относительные ошибки, метеорологи могут оценить надежность прогнозов и эффективно донести их до общественности.
В финансовом мире абсолютные и относительные ошибки играют важную роль в оценке эффективности инвестиций. Инвесторы и финансовые аналитики часто сравнивают фактическую доходность инвестиций с ожидаемой доходностью. Расчет абсолютной и относительной ошибки позволяет им определить уровень отклонения от ожидаемых показателей и принять обоснованные решения относительно инвестиций.
Абсолютная и относительная погрешности особенно актуальны в диагностическом тестировании, а также в области медицины. При проведении тестов или анализе медицинских данных врачам и исследователям необходимо обеспечить точность результатов. Вычисление абсолютной и относительной погрешности позволяет оценить точность и достоверность тестов и на основе полученных данных поставить точный диагноз или сделать выводы.
В целом, абсолютная и относительная погрешность находит реальное применение в самых разных сценариях реальной жизни в различных отраслях. Проектирование мостов, прогнозирование погоды, анализ эффективности инвестиций, проведение медицинских тестов - понимание и расчет этих погрешностей может помочь специалистам принимать обоснованные решения и повысить точность их работы.
Числовые примеры
Чтобы лучше понять концепцию абсолютных и относительных погрешностей, рассмотрим несколько числовых примеров.
Пример 1:
Предположим, длина карандаша измеряется как 15 сантиметров. Известно, что фактическая длина карандаша составляет ровно 14 сантиметров. Чтобы вычислить абсолютную погрешность, вычтите фактическую длину из измеренной: 15 см - 14 см = 1 см; следовательно, абсолютная погрешность в данном случае равна 1 см.
Чтобы рассчитать относительную погрешность, разделите абсолютную погрешность на фактическую длину и умножьте на 100%: (1 см / 14 см) x 100% ≈ 7. 14%. Таким образом, относительная ошибка в данном случае составляет примерно 7,14%.
Пример 2:
Предположим, вы измеряете температуру в комнате, и термометр показывает 25 градусов Цельсия. Вы знаете, что фактическая температура в комнате, измеренная более точным прибором, составляет ровно 24°C. Чтобы рассчитать абсолютную погрешность, вычтите фактическую температуру из измеренной: 25°C - 24°C = 1°C. Таким образом, абсолютная погрешность в данном случае составляет 1 градус Цельсия.
Чтобы рассчитать относительную погрешность, разделите абсолютную погрешность на фактическую температуру и умножьте на 100%: (1°C / 24°C) x 100% ≈ 4,17%. Поэтому относительная погрешность в данном случае составляет примерно 4,17%.
Пример 3:.
Представьте, что вы вычисляете площадь прямоугольного поля. Длина поля составляет 10 метров, а ширина - 5 метров. По данным съемки, фактическая площадь поля составляет ровно 50 квадратных метров. Чтобы рассчитать абсолютную погрешность, вычтите фактическую площадь из расчетной: (10 м x 5 м) - 50 м² = 0 м². Таким образом, абсолютная ошибка в данном случае равна 0 м².
Поскольку абсолютная погрешность равна нулю, относительная погрешность не может быть рассчитана, так как она предполагает деление на ноль. Это означает, что вычисленная площадь точно равна фактической площади. Другими словами, в данном случае ошибки нет.
Эти примеры показывают, как абсолютная и относительная погрешности могут быть рассчитаны в различных сценариях, и подчеркивают важность понимания этих понятий при работе с числовыми данными.
Важность абсолютной и относительной погрешности
Понятия абсолютной и относительной погрешности важны в различных областях, включая математику, естественные науки, инженерное дело и статистику. Эти меры погрешности дают ценное представление о точности и аккуратности математических расчетов, научных экспериментов и анализа данных.
Абсолютная погрешность описывает величину разницы между измеренным или вычисленным значением и истинным или допустимым значением. Она помогает количественно определить степень расхождения и позволяет проводить сравнения между различными измерениями или расчетами. Абсолютная погрешность особенно полезна при работе с физическими величинами с определенными единицами измерения, такими как расстояние, время или температура.
Относительная погрешность, с другой стороны, рассматривает отношение абсолютной погрешности к истинному или принятому значению. Она дает представление о точности измерения или вычисления относительно величины измеряемой или вычисляемой величины. Относительная погрешность особенно важна при сравнении наборов данных или проведении статистического анализа. Она позволяет проводить осмысленные сравнения между величинами с разными порядками величины.
Понимание и расчет абсолютных и относительных погрешностей помогает определить источники неопределенности, оценить надежность данных или результатов и оценить работу измерительных приборов или методов расчета. Благодаря количественному определению ошибок, связанных с процессом, ученые, инженеры и исследователи могут принимать обоснованные решения, улучшать дизайн экспериментов и оптимизировать математические алгоритмы.
Важность абсолютной и относительной погрешности выходит за рамки научной и инженерной областей. В повседневной жизни эти понятия находят применение в различных ситуациях, таких как измерение ингредиентов для приготовления пищи, оценка расстояний во время путешествий и оценка точности финансовых расчетов. Распознавая потенциальные ошибки и их последствия, люди могут делать более обоснованный выбор и обеспечивать качество и надежность своих измерений и расчетов.
Преимущества и применение
Онлайн-калькуляторы абсолютных и относительных погрешностей имеют широкий спектр преимуществ и применений в различных областях. Эти калькуляторы обычно используются в научных исследованиях, инженерном деле и анализе данных для определения точности и прецизионности измерений или вычислений.
Одним из основных преимуществ использования этих онлайн-калькуляторов является то, что они обеспечивают быстрый и удобный способ вычисления и сравнения погрешностей различных измерений или вычислений. Это помогает исследователям и ученым принимать обоснованные решения и делать надежные выводы на основе точных данных.
Еще одно важное применение онлайн-калькуляторов абсолютных и относительных погрешностей - контроль качества и тестирование. Рассчитывая ошибки в производственных процессах или результатах экспериментов, компании могут определить области для улучшения и гарантировать, что их продукция или процессы соответствуют желаемым спецификациям.
Эти калькуляторы также полезны для преподавания и обучения. Они помогают учащимся понять концепцию погрешности и ее важность в научных измерениях. Используя эти калькуляторы, студенты могут практиковаться в вычислении и интерпретации погрешностей и улучшать свои навыки анализа и критического мышления.
Кроме того, онлайн-калькуляторы абсолютных и относительных погрешностей также используются для финансового анализа и прогнозирования. Рассчитывая ошибки в экономических или финансовых моделях, аналитики могут оценить точность и надежность прогнозов. Это позволяет компаниям и инвесторам принимать соответствующие решения, основанные на реалистичных ожиданиях.
В целом, онлайн-инструменты для расчета абсолютных и относительных погрешностей имеют множество преимуществ и разнообразное применение в различных областях. Они полезны для исследований, контроля качества, образования и финансового анализа, предоставляя точные измерения и ценные сведения. Эти калькуляторы являются одинаково ценными инструментами как для профессионалов, так и для студентов, повышая точность и аккуратность анализа данных.
Веб-сайты и инструменты
В Интернете существует несколько веб-сайтов и инструментов, помогающих рассчитать абсолютные и относительные погрешности. Эти ресурсы полезны для студентов, исследователей и профессионалов в различных областях, включая математику, физику и инженерное дело. Ниже перечислены некоторые популярные веб-сайты и инструменты.
Онлайн-калькуляторы: существует ряд сайтов, предлагающих онлайн-калькуляторы, специально разработанные для расчета абсолютных и относительных погрешностей. Эти калькуляторы позволяют вводить фактические и измеренные значения, после чего рассчитываются абсолютные и относительные погрешности.
Электронные таблицы: для расчета абсолютных и относительных погрешностей можно также использовать такие программы, как Microsoft Excel или Google Sheets. Просто введите необходимые формулы и данные, и вычисления легко выполняются для получения значений погрешности.
Функциональные калькуляторы: большинство функциональных калькуляторов имеют возможность вычисления абсолютной и относительной погрешности. Эти калькуляторы портативны и позволяют легко выполнять расчеты на ходу.
Помимо этих сайтов и инструментов, существует ряд учебников и образовательных ресурсов, которые подробно объясняют понятия абсолютной и относительной погрешности. Эти ресурсы обеспечивают более глубокое понимание темы и помогают эффективно использовать веб-сайт и инструменты.
При выполнении расчетов, связанных с абсолютными и относительными погрешностями, важно использовать надежные ресурсы. Всегда перепроверяйте точность используемого веб-сайта или инструмента и при необходимости обращайтесь к нескольким источникам информации. Это поможет обеспечить точность расчетов и предотвратить возможные ошибки и неточности.

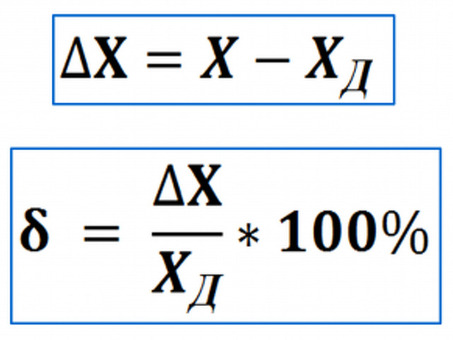



Комментарии