При проведении измерений в научных экспериментах или в повседневной жизни важно понимать концепцию погрешности. Поскольку не существует абсолютно точного измерения, понимание различных типов погрешностей помогает оценить надежность измерения.
Абсолютная погрешность измеряет, насколько расчетное или оценочное значение далеко от истинного значения. Обычно она выражается как разница между измеренным и истинным значением. Абсолютная погрешность может быть положительной или отрицательной, в зависимости от того, больше или меньше истинного значения измеренное значение.
Относительная погрешность, с другой стороны, является мерой точности измерения относительно истинного значения. Она обычно выражается в процентах или долях. Относительная погрешность рассчитывается путем деления абсолютной погрешности на истинное значение и умножения на 100. Она обеспечивает стандартизированный способ сравнения измерений в различных единицах или шкалах.
Стандартная ошибка - это статистическая мера, которая количественно определяет величину вариации или неопределенности в наборе измерений. Она рассчитывается как стандартное отклонение измерений, деленное на квадратный корень из объема выборки. Стандартные ошибки особенно полезны в научных экспериментах для определения точности и надежности результатов.
Понимание и правильная интерпретация различных типов погрешностей измерений имеет решающее значение для точных и надежных научных исследований. Абсолютные, относительные и стандартные погрешности дают ценное представление о точности, аккуратности и неопределенности измерения. Принимая во внимание эти типы погрешностей, ученые могут делать обоснованные выводы из данных и принимать обоснованные решения на основе полученных результатов.
Абсолютная погрешность.
Абсолютная погрешность - это мера того, насколько далеко измерение находится от своего истинного или допустимого значения. Она представляет собой величину разницы между измеренным и истинным значением, независимо от направления. Абсолютная погрешность определяется следующим уравнением.
Абсолютная погрешность = |измеренное значение - истинное значение|.
Абсолютная погрешность всегда выражается в тех же единицах, что и измеренное значение. Она дает информацию о точности измерения и помогает оценить качество полученных данных.
Важно отметить, что абсолютная ошибка не указывает направление ошибки, т.е. является ли измеренное значение слишком высоким или слишком низким по сравнению с истинным значением. Она указывает только на величину разницы. Чтобы определить направление ошибки, необходимо учитывать знак разницы (положительный или отрицательный).
Абсолютная погрешность часто используется в науке, инженерии и других областях, где важны точные измерения. Она позволяет исследователям и экспериментаторам оценить надежность и достоверность данных и помогает выявить систематические или случайные ошибки, которые могут присутствовать в процессе измерения.
Например, если в лабораторном эксперименте известно, что истинное значение измеряемой величины равно 10, а измеренное значение оказалось равным 9,5, то абсолютная погрешность составляет 0,5 единиц. Это означает, что измеренное значение находится на 0,5 единицы дальше от истинного значения, но не уточняется, выше оно или ниже.
В целом, абсолютная погрешность представляет собой количественную меру отклонения между измеренным значением и истинным значением. Она является полезным инструментом для оценки точности и надежности измерений и играет важную роль в научных и экспериментальных исследованиях.
Относительная погрешность
Относительная погрешность - это мера точности измерения относительно истинного значения. Она рассчитывается путем деления абсолютной погрешности на истинное значение, умножения на 100 и выражения в процентах. Относительная погрешность учитывает величину измеряемой величины и позволяет проводить сравнения между измерениями различных величин.
При использовании относительной погрешности важно иметь известное истинное значение для сравнения с измеренным значением. Это истинное значение представляет собой наиболее точное значение, которое может быть получено для измеряемой величины. Затем можно рассчитать относительную погрешность, чтобы определить, насколько близко измеренное значение к истинному.
Относительная погрешность полезна в научных и инженерных приложениях, где важна точность измерений. Она позволяет оценить точность измерений и помогает выявить систематические смещения и ошибки в процессе измерения. Анализируя относительную погрешность, можно внести коррективы для повышения точности и надежности измерений.
Одно из распространенных применений относительной погрешности - сравнение экспериментальных и теоретических значений. Рассчитывая относительную погрешность, ученые могут оценить согласие между двумя значениями и судить о достоверности теоретической модели. Небольшая относительная ошибка указывает на то, что измеренные и теоретические значения находятся в хорошем согласии, в то время как большая относительная ошибка указывает на наличие разногласий и необходимость дальнейшего исследования.
В целом, относительная погрешность дает представление о точности измерения относительно истинного значения. Сравнивая относительную погрешность различных измерений, ученые и инженеры могут оценить их точность и улучшить их для получения более точных результатов.
Стандартная погрешность
Стандартная ошибка - это мера точности статистической оценки. Она представляет собой среднюю величину изменчивости или неопределенности, связанную с оценкой. Другими словами, она определяет степень соответствия выборочной оценки фактическим параметрам популяции.
Для расчета стандартной ошибки необходимо знать объем выборки и изменчивость данных. Формула для расчета стандартной ошибки зависит от типа рассчитываемой статистической оценки, например, среднего значения или доли.
Стандартные ошибки часто используются для построения доверительных интервалов, которые представляют собой диапазон значений, в который, скорее всего, укладывается истинное значение популяции. Меньшая стандартная ошибка указывает на то, что оценка более точная, а доверительный интервал более узкий.
Важно отметить, что стандартная ошибка - это не то же самое, что стандартное отклонение. В то время как стандартное отклонение измеряет дисперсию отдельных точек данных вокруг среднего значения, стандартная ошибка измеряет дисперсию оценок выборки вокруг истинного параметра популяции.
Интерпретация стандартных ошибок важна для понимания надежности и точности статистических оценок. Чем больше стандартная ошибка, тем выше неопределенность и ниже точность оценки. И наоборот, меньшая стандартная ошибка указывает на то, что точность оценки более надежна.

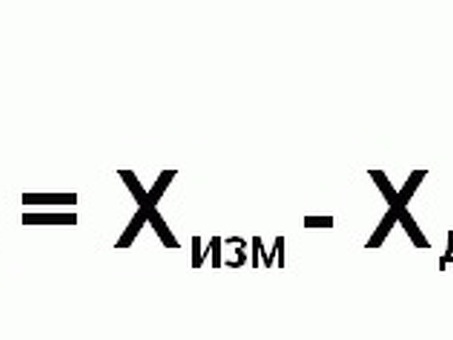



Комментарии