Затрудняетесь перевести двоичные числа в десятичные? Не останавливайтесь на достигнутом! Наш удобный конвертер двоичных чисел в десятичные облегчит вам работу.
Выполните несколько простых шагов, и вы сможете быстро и точно перевести любое двоичное число в десятичную систему счисления. В качестве примера рассмотрим 10111001.
Сначала разделим двоичное число на отдельные цифры.
1
0
1
1
1
0
0
1
Затем присвоим каждой цифре степень 2 от правой части так, чтобы крайняя правая цифра была равна 2^0.
1 * 2^7
0 * 2^6
1 * 2^5
1 * 2^4
1 * 2^3
0 * 2^2
0 * 2^1
1 * 2^0
Теперь просто вычислим значение каждого члена.
1 * 2^7 = 128
0 * 2^6 = 0
1 * 2^5 = 32
1 * 2^4 = 16
1 * 2^3 = 8
0 * 2^2 = 0
0 * 2^1 = 0
1 * 2^0 = 1
Суммируем все вычисленные значения.
128 + 0 + 32 + 16 + 8 + 0 + 0 + 0 + 1 = 185
Таким образом, двоичное число 10111001 равно десятичному числу 185.
Освободите себя от необходимости ручного преобразования и попробуйте воспользоваться удобным конвертером двоично-десятичных чисел. Он работает быстро, легко и точно.
Важность преобразования двоично-десятичных чисел в десятичные
Что такое двоично-десятичное преобразование?
Двоично-десятичное преобразование - это процесс преобразования двоичного числа, представленного в виде двоичного числа, в десятичное число, представленное в виде десятичного числа; двоичное число состоит только из цифр 0 и 1, а десятичное число состоит из цифр 0-9.
Почему важно преобразование двоичной системы в десятичную?
Двоично-десятичное преобразование - важный навык в информатике и цифровой электронике. Оно позволяет понимать двоичные данные и манипулировать ими, что является основополагающим в таких областях, как программирование, сетевые технологии и компьютерная архитектура.
Преобразование двоичных чисел в десятичные облегчает интерпретацию и манипулирование данными, которые они представляют. Например, преобразование двоичных чисел в десятичные позволяет вычислять адреса в памяти, выполнять арифметические операции, интерпретировать IP-адреса и маски подсети.
Как преобразовать двоичные числа в десятичные
Чтобы преобразовать двоичное число в десятичное, выполните следующие действия
- Начните с крайней правой цифры двоичного числа.
- Присвойте вес каждой цифре, начиная с 2.0Удвойте вес крайней правой цифры и удвойте вес каждой последующей цифры.
- Умножить каждую цифру на соответствующий вес.
- Суммируйте произведение, чтобы получить десятичное число.
Например, преобразуйте двоичное число 10111001 в десятичное.
| Двоичное число | Вес. | Продукт |
|---|---|---|
| 1 | 27 | 128 |
| 0 | 26 | 0 |
| 1 | 25 | 32 |
| 1 | 24 | 16 |
| 1 | 23 | 8 |
| 0 | 22 | 0 |
| 0 | 21 | 0 |
| 1 | 20 | 1 |
| Сумма: | 185 | |
Следовательно, двоичное число 10111001 равно десятичному числу 185.
Выводы.
Преобразование двоичных чисел в дробные является фундаментальным понятием в информатике и цифровой электронике. Оно позволяет манипулировать двоичными данными и интерпретировать их в осмысленном виде. Понимание того, как преобразовывать двоичные числа в десятичные, позволяет выполнять вычисления, манипулировать данными и решать задачи в самых разных областях техники.
Понимание двоичной и дробной систем
Введение.
Задумывались ли вы когда-нибудь, как компьютеры представляют числа и выполняют вычисления? Ответ кроется в понимании двоичной и десятичной систем. Эти две системы являются основополагающими для компьютерной науки и техники. В данной статье рассматриваются основы двоичной и дробной систем и их взаимосвязь.
Двоичные системы
Двоичные системы - это числовые системы, в которых используются только две цифры, 0 и 1. Они лежат в основе всех цифровых систем, включая компьютеры. Каждая цифра в двоичном числе называется битом, который представляет собой двоичный разряд.
Двоичные числа основаны на мощности 2. Каждая цифра в двоичном числе представляет собой мощность 2, начиная с самого главного числа, например 2^0, затем 2^1, 2^2 и т.д. Например, двоичное число 1010 представляет собой (1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (0 * 2^0).
Десятичная система
Десятичная система - это наиболее распространенная в нашей повседневной жизни система счисления, в которой используется 10 цифр: 0-9. Каждое десятичное число представляет собой степень 10, начиная с крайней правой цифры, например 10^0, затем 10^1, 10^2 и т.д. Например, десятичное число 247 представляет собой (2 * 10^2) + (4 * 10^1) + (7 * 10^0).
Преобразование двоичных и десятичных чисел
Преобразование двоичного числа в десятичное или наоборот представляет собой простой процесс. При переводе из двоичной системы в десятичную каждое число перед суммированием умножается на соответствующую степень 2. При переводе из десятичной системы счисления в двоичную десятичное число многократно делится на 2, а остаток от каждого шага является двоичной цифрой.
Выводы.
Понимание двоичной и десятичной систем счисления необходимо всем, кто интересуется информатикой и техникой. Эти системы лежат в основе цифровых коммуникаций и вычислений. Усвоение понятий двоичной и десятичной систем счисления позволяет работать с компьютерами и понимать, как они представляют числа и манипулируют ими.
Преимущества перевода двоичных чисел в десятичные
1. Улучшение понимания:
Преобразование двоичных чисел в десятичные помогает лучше понять суть двоичных чисел и взаимосвязь между двоичной и десятичной системами. Это позволит лучше понять, как компьютеры и цифровые системы обрабатывают и хранят информацию.
2. разборчивость:
Десятичные числа обычно легче читаются человеком по сравнению с двоичными. Преобразование двоичных чисел в десятичные позволяет представить их в формате, который легче понять и интерпретировать. Это особенно полезно при работе с большими числами или при передаче их другим пользователям.
3. совместимость с десятичными системами:
Во многих системах и приложениях, таких как финансовые расчеты, анализ данных и языки программирования, преимущественно используется десятичная дробь. Преобразование двоичных чисел в десятичные облегчает работу различных платформ и инструментов за счет беспрепятственной интеграции двоичных и десятичных систем.
4. Точное представление:
Десятичные числа обеспечивают более точное представление дробных значений по сравнению с двоичными. Преобразование двоичных чисел в десятичные позволяет точно представлять десятичные дроби и манипулировать ими, что очень важно в различных областях, таких как наука, инженерия и финансы.
5. привычность и простота использования:
Десятичные числа широко используются в повседневной жизни, что делает их более привычными и удобными в работе для большинства людей. Преобразование двоичных чисел в десятичные позволяет использовать имеющиеся знания о десятичных точках и делает вычисления, сравнения и преобразования более интуитивными и удобными.
| Двоичная система | Десятичная система счисления. |
|---|---|
| 10111001 | 185 |
Что представляет собой двоичное число 10111001 в десятичной системе счисления?
Двоичное число 10111001 представляет собой десятичную систему счисления 185.
Как преобразовать двоичное число 10111001 в десятичную точку?
Для преобразования двоичного числа 10111001 в десятичную точку можно использовать позиционную систему счисления. Каждая цифра в двоичном числе представляет собой степень 2. Начиная с крайней правой цифры, каждый разряд возводится в степень двойки и умножается на силу в данной позиции, чтобы сложить результат. В данном случае вычисление выглядит так: 1 * 2^7 + 0 * 2^6 + 1 * 2^5 + 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 0 * 2^1+ 1 * 2^0 = 128 + 0 + 32 + 16 + 8 + 0 + 0 + 0 + 1 = 185.
Чему равен десятичный эквивалент двоичного числа 10111001?
Десятичный эквивалент двоичного числа 10111001 равен 185.
Помогите, пожалуйста, перевести двоичное число 10111001 в десятичную систему счисления.
Конечно! Чтобы перевести двоичное число 10111001 в десятичную систему счисления, можно воспользоваться позиционной системой счисления. Каждое число представляет собой степень 2, начиная с крайнего правого числа. Умножьте каждое число на 2, возведите его в степень в данной позиции и сложите результат. В данном случае вычисления выглядят так: 1 * 2^7 + 0 * 2^6 + 1 * 2^5 + 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 0 * 2^1 + 1 * 2^0 = 128 + 0 + 32 + 16 + 8 + 0 + 0 + 0 + 1 = 185; следовательно, десятичный эквивалент двоичного числа 10111001 равен 185.
Существует ли десятичный эквивалент для двоичного числа 10111001 185?
Да, десятичное представление двоичного числа 10111001 действительно равно 185.
Как преобразовать двоичное число 10111001 в десятичный эквивалент?
Двоичное число 10111001 можно преобразовать в десятичный эквивалент, используя позиционную нотацию. Каждая цифра в двоичном числе представляет собой степень 2, начиная с самой правой. Умножьте каждое число на 2, возведите его в степень в данной позиции и сложите результат. В данном случае вычисление выглядит так: 1 * 2^7 + 0 * 2^6 + 1 * 2^5 + 1 * 2^4 + 1 * 2^3 + 0 * 2^2 + 0 * 2^1+ 1 * 2^0 = 128 + 0 + 32 + 16 + 8 + 0 + 0 + 0 + 1 = 185. Таким образом, десятичное представление двоичного числа 10111001 равно 185.

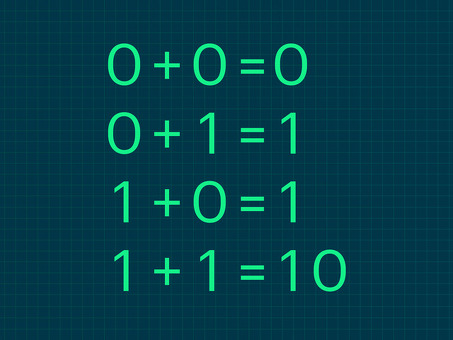




Комментарии