Диплом Dele: экзамены , уровни , основные требования , порядок аттестации , d b 2.
5904.00 ₽
Февраль 16, 2023
21
D b 2
a) Докажите, что площадь выпуклого четырехугольника ABCD можно вычислить по следующей формуле
S 2 = ( p - a )( p - b )( p - c )( p - d ) - abcd cos 2 (( B + D )/2),.
где p - половина окружности, a, b, c, d - длины сторон. b) Докажите, что если четырехугольник ABCD вписан, то S 2 = ( p - a )( p - b )( p - c )( p - d ). c) Если четырехугольник ABCD вписан, то S 2 = abcd sin 2 (( B + D )/2). .
Решение.
a) Пусть AB = a, BC = b, CD = c и AD = d. Очевидно, что S = S ABC + S ADC = (ab sin B + cd sin D )/2 и a 2 + b 2 - 2 ab cos B = AC 2 = c 2 + d 2 - 2 cd cos D. Поэтому.
16 S 2 = 4 a 2 b 2 - 4 a 2 b 2 cos 2 B + 8 abcd sin B sin D + 4 c 2 d 2 - 4 c 2 d 2 cos 2 D , ( a 2 + b 2 - c 2-d 2 ) 2 + 8 abcd cos B cos D = 4 a 2 b 2 . cos 2 B + 4 c 2 d 2 cos 2 D .
Подставляя первое уравнение во второе, получаем
16 S 2 = 4( ab + cd ) 2 - ( a 2 + b 2 - c 2 - d 2 ) 2 - 8 abcd (1 + cos B cos D - sin B sin D ).
Очевидно, что 4( ab + cd ) 2 - ( a 2 + b 2 - c 2 - d 2 ) 2 = 16( p - a )( p - b )( p - c )( p - d ) и 1 + cos B cos D - sin B sin D = 2 cos 2 (( B + D )/2). b) Если ABCD - вписанный квадрат, то B + D = 180 o Поэтому cos 2 (( B + D )/2). )/2) = 0. c) Если ABCD - четырехугольник, то a + c = b + d , следовательно, p = a + c = b + d и p - a = c , p - b = d , p - c = a , p - d = b. Таким образом, S 2 = abcd (1 - cos 2 (( B + D )/2)) = abcd sin 2 (( B + D )/2). Если четырехугольник ABCD является одновременно вписанным и вписанным, то S 2 = abcd .
Источники и прецеденты использования
Книга Автор Прасолов В. В. Год издания 2001 Название Планиметрия Издательство МЦНМО Издание 4* Задачи по главе 4 Название Тема Площадь Номер параграфа 7 Название Площадь четырехугольника Тема Площадь четырехугольника Задание № 04. 045
Этот проект поддерживается и . Диплом Дере:. экзамены , уровни , основные требования , порядок аттестации
Диплом по испанскому языку как иностранному - это официальный документ, выданный Министерством образования, культуры и спорта Испании, признающий уровень знаний и владения испанским языком. Учреждения, ответственные за организацию. экзаменов Испанским центром является Институт Сервантеса, а Университет Саламанки в Испании отвечает за подготовку, корректуру и окончательную оценку всех диссертаций. экзаменов . Как подготовиться к dele ? Мы даем вам возможность подготовить ? к экзаменам Диплом Dele. по испанскому языку как иностранному, выбрав лучшую школу испанского языка, которая предлагает курсы для подготовки к диплому Dele. по испанскому языку как иностранному. три уровня В зависимости от уровня владения языком: ?
Деле (уровень начинающих - B1). Это доказывает, что студент владеет испанским языком на достаточном уровне, чтобы понимать и общаться в простых повседневных ситуациях.
Испанский диплом (средний уровень - B2) подтверждает, что студент владеет испанским языком на достаточном уровне для общения в различных повседневных ситуациях и коммуникативных ситуациях, не требующих использования специальной лексики.
Продвинутый уровень (C2) демонстрирует приобретение достаточных навыков испанского языка для использования в широком спектре ситуаций, требующих высокого уровня знания испанского языка. уровня Языковые навыки и знание социокультурных реалий отражаются в языке.
На этих страницах вы найдете всю информацию, которую необходимо знать и записывать экзамен Деле, из любой точки мира.
Условия и требования Пас. экзамен Dele
Каждый, кто хочет дать из экзаменов Дележ испанского языка должен требования :
При регистрации предоставить доказательства гражданства в стране, где испанский не является официальным языком.
Зарегистрироваться и оплатить за экзамен Отправляйтесь в центр регистрации.
Граждане Испании, проживающие в странах, где испанский не является официальным языком, могут зарегистрироваться. экзамена Если они выполняют, по крайней мере, два из следующих условий и заявляют об этом в письменном виде:.
Испанский язык не является родным языком их родителей.
Испанский не является их первым иностранным языком.
Испанский язык не является языком повседневного использования.
Ваше обучение было не на испанском языке.
Сроки экзамена по испанскому Dele
Регистрация на получение диплома Деле начинается примерно за два месяца до начала обучения. до экзамена Его продолжительность составляет примерно один месяц.
Правила участия
Документы, необходимые для регистрации на каждый из них. из экзаменов Dele:
можно получить в центре регистрации и заполнить очень внимательно. Примечание: В дипломе, который вы получите в конце, указано имя зарегистрированного лица, как указано в регистрационной форме.
Оригинал и копия документа, удостоверяющего личность, должны содержать как минимум следующую информацию: имя и фамилию, гражданство, дату и место рождения. Примечание: Данные, указанные в форме участия, должны быть полностью согласованы в документе, удостоверяющем личность.
Письменное заявление (в зависимости от каждого конкретного случая) с указанием как минимум двух условий, установленных для граждан Испании, проживающих в странах, где испанский язык не является официальным. После регистрации. на экзамен Каждый человек получает по почте копию бланка с отметкой о его регистрационном номере и информацией о месте, дате и времени. экзамена .
Документы, необходимые для доставки экзамена Dele
Желающие пройти экзамен Dele, должны прийти на экзамен Кандидаты должны принести следующие документы
Копия регистрационной формы с печатью.
Удостоверение личности (то же, что и при регистрации).
Получено письмо-приглашение от Центра зачисления Деле.
Cборы за сдачу экзамена Dele
Существует два способа оплаты экзаменационного взноса за уровень Dele
Наличными или банковским чеком. Лично в центре, где проходит регистрация.
Чеком или банковским переводом. Средства должны быть перечислены на счет, который можно получить в регистрационном центре. Те, кто выбрал этот вариант оплаты, должны предъявить доказательство оплаты экзаменационного взноса во время регистрации.
Стоимость экзаменов зависит от страны и валюты. и экзамена (*):
Запишитесь на консультацию.
Экзамен Certificado Inicial de Español (C. I. E.) - начальный уровень B1
Сертификат Certificado Inicial de Español B1 подтверждает языковые способности, достаточные для понимания и адекватного реагирования на наиболее распространенные жизненные ситуации, а также для выражения желаний и потребностей на базовом языке. уровне . Обследование для получения этого. уровня Он состоит из следующих частей
Часть 1: Понимание текста.
(40 минут) Два типа заданий: a. Кандидаты должны ответить на вопрос в информационном тексте, выбрав правильный ответ из предложенных ответов (множественный выбор). b. Кандидаты должны найти правильный ответ на вопрос, заданный в тексте. c. Кандидаты должны найти правильный ответ на вопрос в информационном тексте, выбрав правильный ответ из предложенных ответов (множественный выбор). Демонстрационную версию в формате PDF можно найти здесь.
Часть 2: Текстовое представление
(50 минут) Цель - написать короткие, простые предложения практического характера. PDF-версию демонстрации, включая примечания и сообщения, можно найти здесь.
Часть 3: Слушание.
(30 минут) В течение этого времени кандидаты должны выполнить четыре упражнения на простые разговоры или записанную информацию. Они должны выбрать правильный ответ из предложенных. Демонстрацию в формате PDF можно найти здесь.
Часть 4: Грамматика и лексика
(40 мин) Три задачи:
Кандидаты должны соотнести предложение с соответствующей ситуацией.
Кандидаты должны найти в предложении слова и фразы, которые не соответствуют контексту.
Кандидаты должны завершить текст, выбрав правильный вариант.
Вы можете найти демо-версию в формате PDF здесь.
Часть 5: Обсуждение
(10 минут) За десять минут до начала обсуждения кандидат получает лист с пиктограммой и описанием ситуации, которую он будет обсуждать. Нажмите здесь, чтобы получить пробную версию в формате PDF.
Diploma Básico de Español (D. B. E.) - промежуточный уровень B2
El Diploma Básico de Español B2 демонстрирует достаточную языковую компетенцию для управления повседневными ситуациями в обычных повседневных ситуациях, не требующих лингвистических знаний. Обследование для получения этого. уровня Он состоит из следующих частей
Часть 1: Понимание текста.
(60 минут) Кандидаты должны ответить на 12 вопросов (множественный выбор) по четырем текстам (до 450 слов каждый). Демо-версия в формате PDF доступна здесь.
Часть 2: Текстовое представление
(60 минут) Кандидаты должны написать личное письмо или короткое эссе объемом не более 150-200 слов каждое. Демонстрационный материал в формате PDF доступен здесь.
Часть 3: Слушание.
(30 минут) Кандидатам предоставляются четыре записи, включающие сообщение, новости, дискуссию или интервью. Кандидаты должны ответить на 12 вопросов (множественный выбор). Вы можете найти демо-версию в формате PDF здесь.
Часть 4: Грамматика и лексика
(60 мин) Две задачи:
Заполните 20 пробелов в тексте, выбрав наиболее подходящий ответ из трех предложенных.
Заполните пропуски 40 коротких разговоров и выберите наиболее подходящий ответ.
Вы можете найти демо-версию в формате PDF здесь.
Часть 5: Обсуждение
(10-15 минут) За десять минут до начала дискуссии кандидатам выдается лист с набросками истории и описанием ситуации, о которой они будут говорить. Пробная версия доступна в формате PDF здесь.
Diploma Superior de Español (D. S. E.) - высший уровень C2
El Diploma Superior de Español C2 демонстрирует языковую компетенцию, которая необходима студентам, чтобы чувствовать себя комфортно в ситуациях, требующих высокого уровня языковой компетенции. уровня Использование языка и культурная компетентность. Обследование для получения этого. уровня Он состоит из следующих частей
Часть 1: Понимание текста.
(60 мин) Две задачи:
Кандидаты отвечают на девять вопросов (множественный выбор) по трем текстам (не более 800 слов каждый).
Кандидаты должны составить полный текст из 10 текстов.
Вы можете найти демо-версию в формате PDF здесь.
Часть 2: Текстовое представление
(60 минут) Кандидаты должны написать два разных текста
Письмо (не личное).
Краткое эссе.
Вы можете найти демо-версию в формате PDF здесь.
Часть 3: Слушание.
(45 мин.) Кандидаты должны прослушать двух или более участников и ответить на 16 вопросов (множественный выбор) по четырем текстам, предполагающим обсуждение. Это также комментарий или ссылка на СМИ.PDF Пробную версию можно найти здесь.
Часть 4: Грамматика и лексика
(60 минут) Кандидаты должны выполнить следующие три задания.
Заполните 20 пробелов в тексте, выбрав наиболее подходящий ответ из трех предложенных.
Задание с множественным выбором: выберите наиболее подходящий ответ из трех предложенных и заполните пропуски в 35 предложениях.
Кандидаты должны найти 5 грамматических ошибок в одном или нескольких текстах.
Вы можете найти демо-версию в формате PDF здесь.
Часть 5: Обсуждение
Пройдите эту часть формального экзамена. экзамена Чтобы получить El Diploma Superior DeEspañol, кандидаты должны проконсультироваться с комиссией в течение 10-15 минут Пробная версия PDF доступна здесь.
Экзамены по приобретению диплома Деле работает с делегациями Института Сервантеса по всему миру. диплом Сертификат выдается Министерством образования, культуры и спорта Испании и действителен бессрочно. Испанский диплом является официальным документом о владении языком в соответствии с международными стандартами и признается государственными и деловыми органами, а также академическими учреждениями в Европе и США.
Сервисные центры в Испании
Центр услуг "Испанский на русском" - это ваш путеводитель по обучению в Испании. Выбор учебных заведений, перевод в испанские средние школы, визы, вид на жительство для всех семей, детские лагеря, спорт, школы английского языка.
Теги: испанский,. экзамен dele , подготовка к dele , сдать экзамен dele , экзамен деле, экзамен Испанский язык. dele То, что мы имеем в математике, скромно.
Уравнение - это математическое уравнение, в котором одна или несколько величин неизвестны. Необходимо найти такое значение незнакомца, чтобы при его замене примером возникало подходящее арифметическое равенство.
Например, возьмем уравнение 8 + 4 = 12. Вычисления в левой части уравнения приводят к правильному арифметическому уравнению, т.е. 12 = 12.
Уравнение 8 + x = 12 с неизвестной переменной x, значение которой неизвестно. Результат должен быть таким, чтобы знак равенства был оправдан и левая часть была равна правой.
Степень уравнения можно определить по наибольшей степени, в которой находится неизвестное. Если неизвестное находится во второй степени, то такое уравнение является квадратным уравнением.
Квадратное уравнение имеет вид ax 2 + bx + c = 0. где a - первый или наибольший коэффициент, не равный нулю, b - второй коэффициент и c - свободный член.
Существует три типа квадратных уравнений
Концепция уникальных возможностей
Отличием квадратного уравнения является выражение под корнем типа и является нахождение корня квадратного уравнения. Латинское слово discrimination означает "идентификация" или "дискриминация" и обозначается буквой D.
Эта функция является отличным помощником для подсчета количества корней в уравнении.
В большинстве случаев мужчина используется для поиска незаметной способности: мужчина используется для поиска незаметной способности.
В этом духе универсальный человек, находящий корни квадратного уравнения, выглядит так
Этот тип также подходит для неполных квадратных уравнений.
Но есть и другие типы - все зависит от типа уравнения. Чтобы не перепутать их, сохраните таблицы или распечатайте их и храните в книге.
Как решать квадратные уравнения с помощью отличительных способностей
На уроках алгебры в 8 классе вы можете столкнуться с проблемой нахождения действительных корней квадратного уравнения. Для этого важно найти различие и убедиться, что оно неотрицательно, прежде чем использовать тип. Только после этого можно рассчитать значение корня. Если характеристическая сила отрицательна, то уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения AX 2 + BX + C = 0:.
А вот еще один рабочий лист: здесь вы найдете, кто найдет корни квадратного уравнения, используя определители.
Важно практиковаться, чтобы запомнить и легко использовать алгоритм квадратного уравнения. Вперед!
Примеры квадратных уравнений квадратных уравнений с использованием уникальных способностей
Ответ: корень уравнения равен 3.
Различение квадратных уравнений
Мы уже рассмотрели, как решать квадратные уравнения. Далее рассмотрим более подробно то, что мы называем ненавязчивой способностью квадратных уравнений.
Давайте вернемся к типу и найдем корни квадратного уравнения.
Уравнение 'b 2-4ac' под корнем называется скромным и обозначается буквой 'd'.
Альтернативно, тип нахождения корней квадратного уравнения может быть описан через характеристическую силу следующим образом.
По одной из версий, термин дискриминация происходит от латинского discrimination disorder. Это означает "дискриминация" или "идентификация".
В зависимости от знака 'D' квадратное уравнение может иметь два, один или НЕТ корней; рассмотрим все три случая: квадратное уравнение - это квадратное уравнение, квадратное уравнение - это квадратное уравнение, квадратное уравнение - это квадратное уравнение, квадратное уравнение - это квадратное уравнение.
I случай D >0 (характеристическая емкость больше нуля).
-b±√d2a
-5±√812-2
-5±9 4
1 2
II Случай D = 0 (скромные возможности равны нулю)
d = b 2-4ac d = (-8) 2-4-16-1 d = 64-64 d = 0
-b±√d2a
- (-8) ±√032
8±0 32
8 32
1 4
1 4
III Случай D (тонкий потенциал ниже нуля)
d = b 2-4ac d = (-6) 2-4-9-2 d = 36-72 d = -36 d
-b±√d2a
- (- 6) ±√ -36 32
Ответ: нет действительных корней
Общая информация.
Решение квадратных уравнений является одним из ключевых моментов в математике. Еще древние вавилоняне и греки пытались найти закономерности в решении таких уравнений. Однако именно индийский философ Буджаяма впервые объяснил, как находить квадратные дополнения. Именно он предложил записывать уравнения в виде: ax 2 = c и ax 2 + bx = c. Позже метод был усовершенствован. Например, Евклид предложил метод геометрического вычисления ответа.
Однако самым важным было открытие булева языка. Изучая различные типы уравнений, он пришел к выводу, что почти всегда можно упростить уравнение, заменив переменные другим набором, содержащим новые незнакомые. В этом случае уже не составляет труда определить инициалы, найти их.
Этот метод был также применен к квадратным уравнениям. Используя дискретизацию, теперь можно упростить квадратичную форму, используя две переменные. Это понятие тесно связано с многочленами вида: d(m) = a 0 *m n + a 1 *m n-1 + a 2 *m n-2 + ... + a n-1 * m + a n, где m - искомое неизвестное, a n, a n-1, a n-2, ... a 1 и a 0 - числовые константы.
Термин "дискретная возможность" не был изобретен математиками, но успешно использовался ими для вычисления квадратичных функций. Оно происходит от латинского discriminant formula, что буквально означает "разделение". Важным значением была величина, изобретенная Булем, которая имеет вид B2-4AC. Ученые обнаружили, что поскольку переменные изменялись линейно, заниженная способность была равна исходной заниженной способности, умноженной на член, найденный по поведенческой функции незнакомца.
При решении уравнения, тип которого содержит его отличительный и корневой тип, тип используется для быстрого определения количества возможных решений и числовых выводов. Математически определение записывается следующим образом: p(x) = m + mx +⋯ + mx, m ≠ 0, где d(p) = m∏ (m - m). Другими словами, разность многочлена p(x) является суммой корней с неизвестными коэффициентами в основном поле их существования.
Уникальная концепция компетенции.
Эта функция является одним из эффективных решений квадратного представления. Его можно легко использовать для нахождения количества корней, для которых уравнения существуют или для которых они не существуют. Его можно применять как к полным, так и к неполным уравнениям. Однако последний вариант не требует использования ненавязчивых навыков.
Этот урок изучается в 7 и 8 классах средней школы. Простой пример помогает лучше понять важность параметров: предположим, у нас есть уравнение вида m 2 + 2 m-8 = 0. Без всякого смысла предположим, что решение уравнения сводится к сокращению выражения квадратного корня m 2 + 2m +1-1-8 до выражения = 0. Результат складывается с нулем, поэтому можно прибавлять и отнимать.
В общем, все эти преобразования могут быть выполнены в следующем порядке
В качестве разбиения был выбран полином B2-4AC. Это уравнение, по сути, определяет существование решения и количество корней. После выполнения расчета ответ на уравнение является фактическим.
Отношения параметров.
Объяснение дискриминанта имеет и графическое обоснование. Физически задача заключается в комплексном подходе установления взаимосвязи. Фактически это фиксирование нулей параболы уравнения, то есть точек, в которой она пересекает ось абсциссы. Знак при переменной в квадрате будет определять положение веток параболы. Они будут идти вверх при a >0, а выражения x1 = (- b +√b2-4 ac) / 2a, x2 = (b-√b2-4 = (b +√b2-4 ac) / 2a в случае 2-4 ac двойного слагаемого произведения первого множителя 2a. Минорное выражение называется видом сокращенного усмотрения.
Идентификация при нахождении корней уравнения может принимать три значения.
Последнее выражение является разновидностью корня квадратного уравнения; его можно использовать для решения уравнений с двумя степенями. Через характерные, более крупные корни уравнения. порядков . Для этой цели используются методы снижения класса в квадратах. Однако студенты начинают учиться такому поведению, когда в прошлом году их учили решать уравнения с шумом порядка .
Формальный пример.
Даже если учащиеся знают правило поиска корней с ненавязчивой силой, они не могут научиться быстро вычислять корни уравнения без практики. Поэтому решение реальных проблем является неотъемлемой частью школьной программы.
Определите разрешимость уравнения 4m 2 - 2m - 3 = 2. Для удобства две из них нужно сдвинуть влево. Результат: 4m 2 - 2m - 5 = 0. Дискриминант равен D = 4 - 4 * 4 * 4 * 4 * (-5) = 4 + 80 = 84. Так как это больше нуля, то корней два. Сложность здесь заключается в том, что не существует целого числа, равного квадратному корню из √84. Однако √84 = √4 * √21 = 2 √21. Используя формулу, получаем m = (2 ± 2√21) / 2 * 4. Удалите двойку в скобках и m = (2 * (1 ± √21) / 2 * 4 = (1 ± √21) / 4. Это выражение является необходимым решением.
Поэтому все выражения имеют тенденцию переформулироваться, чтобы принять классическую форму. Его можно либо умножить или разделить на число, либо найти общий знаменатель. Затем необходимо найти дискриминант. Форма определяет, имеет ли смысл дальше исследовать корни уравнения.
Расчеты на электронно-вычислительной машине
Найти решение уравнения с помощью дискриминанта довольно просто. Необходимо запомнить только два типа и свойства, которые зависят от значения дискриминанта. Однако на практике вы столкнетесь с примерами, включающими интегралы, логарифмы и экспоненциальные функции. Все они могут быть записаны в виде сложных дробей.
При самостоятельном решении проблем, даже если вы обладаете большим опытом и знаниями, вы, скорее всего, допустите ошибки. Именно поэтому при расчете сложных примеров стоит использовать онлайн-калькуляторы.
К числу услуг, которые предлагают такие услуги, относятся
Эти российские сайты. Интерфейс интуитивно понятен. Для выполнения расчетов нет необходимости вводить личные данные или оплачивать услуги. Все, что нужно сделать пользователю, это написать квадратное уравнение в предложенном формате или таблицу, состоящую из них. Программа автоматически выполняет необходимые расчеты и предоставляет пошаговое решение. Кроме того, сайт Equation Solver содержит краткий теоретический материал и стандартные примеры с подробными решениями.
Даже если вы ничего не знаете о дискриминантных коэффициентах, после нескольких применений компьютера вы сможете восполнить пробелы в своих знаниях, научиться самостоятельно решать примеры и узнать, как правильно писать дискриминантные коэффициенты. Использование сайта Maths Solutions позволяет сэкономить время и получить точные результаты.
Квадратичные уравнения. Неочевидность. Теорема Виса.
Математическая теория ???? Уравнения.
Уравнение вида x 2 + b x + c = 0. где a, b и c - произвольные числа с ≠ 0, называется квадратным уравнением. Числа a, b и c называются коэффициентами, где a - первый коэффициент, b - второй коэффициент и c - свободный член.
Квадратное уравнение может иметь не более двух корней. Решение такого уравнения означает, что все корни найдены или доказано, что они есть.
Модерация.
Количество корней в квадратном уравнении зависит от таких факторов, как способность быть скромным (обозначается буквой D).
Нахождение корней квадратного уравнения
Скромная способность - это математический инструмент, позволяющий определить количество корней. Выражается в определенном типе:.
D = B 2-4AC
Пример №1. Решите уравнение x 2-2 x-3 = 0. Найдите коэффициенты: a = 1, b = -2, c = -3. Найдите различие: d = b 2-4ac = (-2) 2-41 (-3) = 4+12 = 16. Это означает, что характеристика положительна, поэтому уравнение имеет два различных корня, которые находятся.
Пример №2. Решите уравнение 5x2 +2x +1 = 0. Определите коэффициенты: a = 5, b = 2, c = 1. d = b 2-4ac = 2 2-4 = 4-20 = -16, d 2-6x+9 = 0. Определите коэффициенты: a = 1, b = 6, c = 9.
D = b 2-4ac = (-6) 2-4 = 36-36 = 0, d = 0, 1 корень
Теорема Бето.
В квадратном уравнении есть места, где первый коэффициент равен 1 (обратите внимание на примеры 1 и 3), такие уравнения называются сокращенными уравнениями.
Уменьшенные уравнения можно решить не только с помощью ненавязчивых способностей, но и с помощью теоремы Бето.
Сумма корней сокращенного уравнения равна второму коэффициенту, полученному с противоположным знаком - произведение корней равно третьему коэффициенту.
Корни по этой теореме находятся вербально с помощью выбранного метода. Рассмотрим это в качестве примера.
Пример №4. Решите уравнение x 2-10x+21 = 0. Напишите коэффициенты: a = 1, b = -10, c = 21. Примените теорему Бето: a = 1, b = -10, c = 21.
Начните с произведения корня, который является положительным числом и оба корня либо отрицательны, либо положительны. Предположим, что это либо 3 и 7, либо их противоположности. Посмотрите на сумму, она является положительным числом и поэтому совпадает с парой чисел 3 и 7. 3+7 = 10, что подтверждает 37 = 21. Поэтому корнями уравнения являются числа 3 и 7.
Пример №5. Решите уравнение: x 2 +5x +4 = 0. Запишите коэффициенты: a = 1, b = 5, c = 4. По теореме Виета: a = 1, b = 5, c = 4.
Поскольку произведение корней равно 4, мы знаем, что оба корня отрицательны или положительны. Мы видим, что сумма отрицательна. Таким образом, мы получаем два отрицательных числа, совпадени е-1 и-4. Давайте проверим:.
Решение квадратных уравнений
Квадратные уравнения изучаются в 8 классе, поэтому в них нет ничего сложного. Совершенно необходимо знать их решения.
Прежде чем рассматривать конкретные методы их решения, следует отметить, что все квадратные уравнения можно условно разделить на три категории.
В этом заключается существенное отличие квадратного уравнения от линейного уравнения, где корни всегда присутствуют и единственны. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь, называемая ненавязчивой способностью.
Модерация.
Вы должны знать это уравнение со стороны. Откуда он берется, теперь не имеет значения. Важно то, что отличительные знаки говорят нам о том, сколько корней имеет квадратное уравнение. В частности.
Примечание: Дискретность показывает количество корней, а не знаков, как многие почему-то думают. Посмотрите, например, и вы убедитесь в этом сами:.
Выпуск. Количество корней имеет квадратное уравнение.
Запишите коэффициенты первого уравнения и найдите способность к дискретизации: a = 1, b = -8, c = 12- d = (-8)2-4-1-12 = 64-48 = 16
Поэтому, поскольку характеристики положительны, уравнение имеет два разных корня. Аналогично анализируется второе уравнение: a = 5, b = 3, c = 7, Δ = 3 2-4-5-7 = 9-140 = -131.
Характеристика является отрицательной и не имеет корней. Последнее уравнение: a = 1, b = -6, c = 9, Δ = (-6) 2-4-9 = 36-36 = 0.
Характеристика равна нулю - корень есть.
Обратите внимание, что коэффициенты написаны для каждого уравнения. Да, это требует времени, да, это утомительно - но вы не запутаете актеров и не наделаете глупых ошибок. Выбор: скорость или качество.
Кстати, когда вы привыкнете к этому, через некоторое время вам не нужно будет писать всех вкладчиков. Вы выполняете такие функции в своем сознании. Большинство людей начинают это делать примерно после 50-70 решенных уравнений - обычно их не так много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D >0, корни можно найти по типу:.
Основные типы корней квадратных уравнений
Первое уравнение: x 2-2 x-3 =0 ⇒ a = 1, b = -2, c = -3, d = (2)2-4-1-(-3) = 16.
D >0 ⇒ Уравнение имеет два корня. Давайте найдем их:.
Второе уравнение: 15-2 x-x 2 =0 ⇒ a = -1, b = -2, c = 15, d = (-2) 2-4-(-1) 15 = 64.
D >0 ⇒ Уравнение снова имеет два корня. Найдите их.
Наконец, третье уравнение: x 2 + 12 x + 36 =0 ⇒ a = 1, b = 12, c = 36, d = 12 2-4-1-36 = 0.
d =0 ⇒ Уравнение имеет корень. Можно использовать любой тип. Например, первый:.
Как видно из примеров, все очень просто. Если вы знаете тип и умеете считать, то проблем не возникнет. Наиболее распространенной ошибкой является замена негативных показателей в СМИ. Опять же, вам поможет вышеописанная техника: посмотрите на СМИ буквально, запишите все шаги и сразу же устраните ошибки.
Неполные квадратные уравнения
Квадратное уравнение может несколько отличаться от уравнения, приведенного в определении. Например:.
Нетрудно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются еще проще, чем стандартные уравнения. Они даже не требуют подсчета идентификационных данных. Теперь давайте введем новое значение.
Конечно, возможен очень сложный случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение имеет вид x 2 = 0. Очевидно, что в таком уравнении существует только один корень. x = 0.
Рассмотрим другой случай: пусть b = 0, тогда мы имеем неполное квадратное уравнение вида ax 2 + c = 0. Давайте немного трансформируем его.
Решение неполных квадратных уравнений
Поскольку квадратный корень арифметический существует только из неотрицательных чисел, последнее равенство имеет смысл только в том случае, если ( - c / a) ≥ 0. Заключение: заключение.
Теперь разберемся с уравнением в форме Ax 2 + Bx = 0, где свободные элементы равны нулю. Это очень просто. Всегда есть два корня. Все, что вам нужно сделать, это проанализировать многочлен на коэффициенты.
Установите общие коэффициенты за скобками
Если хотя бы один из множителей равен нулю, то произведение равно нулю. Именно отсюда берутся корни. Приведем несколько таких уравнений:.
Работа. Решите квадратное уравнение:.
x 2-7 x = 0 ⇒ x - (x - 7) = 0 ⇒ x1 = 0, x 2 = - (- 7)/1 = 7.
5 x 2 + 30 = 0⇒5x 2 =-30⇒x2 = -6. Корня нет, так как квадрат не равен отрицательному числу.
4 x 2-9 =0⇒4x 2 =9⇒x2 =9/4⇒x1 = 3/2 = 1. 5, x 2 = -1. 5. Указания по решению явных
Элемент 0 не принадлежит ни к какому определенному набору. Мы записываем его с круга, но на квадрате. Число 1 принадлежит множествам A и B, но не принадлежит множеству c. Найдем площадь на пересечении множеств a, b и c и запишем это число 1. На пересечении a, b и c найдем предметы 2. и g. Далее опираемся на (1). Области A B C содержат элементы 4 и 8. Область A B C пуста, а область
содержит элемент 7; область ABC содержит элементы 6 и 9; область A B C пуста; область A B C пуста; область A B C содержит элементы 6 и 9.
A 1 B 8 4 7 0 5 Поэтому ответ: C P = 6 2 3 9 Рассмотрим другой пример. Множество P A B C A B C A B C A B C A B C A B C Найдите элементы рис. 2. B = ; C = ; I = . Диаграмма Венна показана на рисунке 2. Из этой диаграммы следует, что P = . 1. 4 Соотношения включения Упрощение теоретико-множественных типов обычно осуществляется путем применения теорем поглощения и адвекции. Однако во многих случаях, учитывая отношение между множествами (равенство, включение и т.д.), упрощение можно продолжить. Проиллюстрируем это на примере множества, заданного следующим уравнением: p a b c c d a c d a b c b c c d . (1) Упростим уравнение (1), используя теоремы поглощения и адвекции: P B C B D A B C A C D . (2) Это множество состоит из четырех элементов: 2) BD ; 3) A B C ; 4) A C D . A Предположим, что множества A , B , C и D связаны друг с другом включением B. Рассмотрим первую компоненту B C множества (2) D. Для B I C , рисунок 1 B C = B . Это можно увидеть на рисунке 2. На рисунке 2 множество B (вертикальная штриховка B) является подмножеством множества C и показано горизонтальной штриховкой. Набор B C имеет горизонтальную и вертикальную штриховку. В то же время две черточки в I представляют собой множество B, поэтому B C = B. То же самое относится и ко второму компоненту множества (2). То есть для B D = B, а для четвертой компоненты A C D = C и C D C для C D. A A A I Наиболее сложным случаем является третья компонента A B C. Выделим пересечения A B. Первая компонента множества (1) - A B C = B. Вторая компонента множества (2) - A C D = B. Третья компонента множества (3) - A C D = B. На рисунке 3 горизонтальная штриховка обозначает набор A, а вертикальная - набор B. Из диаграммы видно, что B , так как области A и B не пересекаются (как и области A и C). Однако если A B = , то C = . A B C D Таким образом, мы находим (2) упрощенное представление всех четырех компонентов I. Подставим их в (2). Рисунок 4 P B C B D A B C A C D =
= b a c b a c. (4) Это представление нарисовано на диаграмме Венна (рис. 4). Область B на диаграмме показана вертикальной штриховкой, а область A C - горизонтальной. Поскольку заштрихованная область - это вся область b a c. Тот же эффект можно получить алгебраически из выражения (4). Прежде всего, заметим, что поскольку a b c, то a c a b b c. Рассмотрим другой пример 2. Упростите выражение p a b c b c d a c d (6), учитывая интеллектуальные соотношения (3). a b c поэтому первый компонент (6) становится a b c a. После b c, d d. b c c Аналогично, a c поэтому d d. c c. Заменим эти выражения в (6). p ab c B C D A C D A C D A C D A C D A C D A C D A C D. Это минимальное выражение (6) для всего случая включения (3). Ответ: a c d. 2. Булевы функции 2. 1. Булевы функции в обычной форме Обычная форма булевых функций включает все типы, задаваемые формулами делимой вертикали (dnf), т.е. сопряженные (произведение суммы). Сопряжение. В этом случае ДНФ может содержать отдельные символы, отличные от ссылок. То же самое относится и к CNFS. Это означает, что тип, представленный в КНФ, может содержать отдельные переменные, не связанные с точкой разделения, вместе с другими переменными вместе с точкой разделения. Примеры нормальных форм: 1) f (a, b, c) ab ab c (расщепленная нормальная форма) -3) f (p, q, r) (p q) r (сопряженная нормальная форма) -2) f (a, b), c, d) (b c d) (c d) (a c d) (сопряженная расщепленная форма, т.е. эта форма является одновременно dnf и cnf) -6) f 1 (константа функции является нормальной формой). (они принадлежат нормальной форме) -7) f 0 (нулевые константы функции также принадлежат нормальной форме).
Они не имеют ничего общего с нормальной формой: 1) f (a, b, c) ab c. Первая сумма не является ссылкой. Функции приведены во втор. форме. порядка ; 2) f (a, b, c, d) (bd c d) (c d) (a c d) (a c d). Эта функция находится в третьей форме и, следовательно, не в обычном виде порядок : Выражение в первой скобке содержит конъюнкции, отличные от отдельных аргументов - 3) f ( A , B , C ) AB A ( B C ). Вторая сумма не является комбинацией отдельных переменных. Эта функция также имеет третью форму. порядка ; 4) f ( A , B ) AB . Это выражение не принадлежит к нормальной форме. порядок Но это не выборы звеньев и не звено выборов - 5) f ( A , B ) A B . Как и в предыдущем случае, это выражение не применимо к нормальной форме - 6) f (A , B , C , D) AB ACD . Если убрать обратную косую черту, то DNF останется. Если используется инвертированный знак, то это выражение заменяется третьим порядка . Взаимно простая совершенная нормальная форма (ДНФ) функции от n переменных - это форма, в которой все сопряженные члены являются минимальными. Здесь минимальный член является сопряженным для n переменных, где каждая переменная включена один раз в прямой или обратной форме. Пример: f ( A , B , C , D ) ABCD ABCD ABCD ABCD ABCD ABCD. Функция зависит от четырех переменных. Каждое звено является минимальным членом, так как оно содержит каждую переменную, от которой зависит функция, один раз. Поэтому функции представлены SDF. f Функции, заданные простыми связями, такими как ( A , B , C , D ) ABCD, также относятся к классу SODNF. Хотя эта ссылка состоит из одного звена, она является минимальным термином. В отличие от этого представления, функция f ( A , B , C , D ) ABD не является СПНФ, поскольку содержит виртуальный аргумент C. Она представлена минимальной ДНФ. Функция f ( A , B , C , D ) ABC ABC ADC ABC похожа на SDNF. Это происходит потому, что все соединения состоят из одних и тех же символов, с инверсией или без нее. Однако это выражение не является SDNF, поскольку функция зависит от четырех переменных, а связи состоят только из трех аргументов каждая. полностью сопряженная нормальная форма ( SPNF ) функции от n переменных - это форма, если все сопряжения являются максерами. максерм - это выборы от n переменных, где каждая переменная включена один раз, либо прямо, либо в инверсной форме. Выборы из n переменных, в которых каждая переменная включается один раз, либо в прямой, либо в инверсной форме. Например, функция f ( A , B , C , D ) ( A B C D ) ( A B C D ) ( A B C D ) зависит от четырех переменных и представлена в виде SCNF. Поскольку все переменные включаются по одному разу в каждое из этих выражений в скобках, выражение в скобках является макросом. Выражение f ( A , B , C , D ) A B C D также относится к категории SCNF, но не содержит круглых скобок. Выбор A B C D содержит все переменные определенной функции, поэтому этот выбор является maxterm. Функции формы
F (a, b, c, d) (a b c d) (a b c) не является scnf. Последнее выражение в скобке не является макстермом, поскольку содержит только три переменные.2. 3. Булевы функции в выражениях с полным расщеплением вертикальной формы могут быть выражены в SCNF с помощью теоремы Шеннона о разложении (как в предыдущей подглаве). Однако, как только СПНФ функции найдена, проще использовать таблицы истинности. Пример 1. Воспроизвести функцию в SPNF. Отсортируйте количество квадратичных членов в порядке возрастания. f (a, b, c) 1) bc; Таблица 1 2) f (a, b, c, d) a bc d; r a b c f 3) f (a, b, c, d) ab (d cd ac); 0 0 0 1 1 0 1 4) f (a, b, c, d) a (bc d abcd abcd); 2 0 1 0 1 5) f (a, b, c, d) ad ac bc. 3 0 1 1 1 1 1 Решение. 4 1 0 0 0 0 0 Первая функция зависит от трех переменных и поэтому строит 5 1 0 0 1 0 таблицу с тремя столбцами a, b и c и записывает 6 1 1 1 0 0 1 двоичный набор. Линейные переменные (Таблица 1). Слева расположите столбец R для записи десятичных эквивалентов двоичного набора. Заполните колонку f. Первый член a равен 1 при a = 0. Поэтому в столбце f расположите единицы на строке с номерами 0-4, т.е. a = 0. = 0. Найдите строку таблицы. Здесь b = 1 и c = 0. Это ряды с номерами 2 и 6. Единицы в столбце f показывают, сколько минералов из столбца r образуют желаемый sdnf. Ответы на первую функцию - 0, 1, 2, 3 и 6. Для второй функции составляется таблица "истина-истина" (табл. 2). Первое слагаемое для этой функции - A. Поэтому заполните столбец f единицами на пересечении строк 8, 9, 10, 11, 12, 13, 14 и 15. Сумма BC равна единице, если B = C = C = 1. Столбец 1, столбец F, заполнен единицами на пересечении строк 6 и 7 (не заполняйте строки 14 и 15, так как они уже содержат единицы, A B C D F.) Добавьте единицу в столбце f, соответствующую третьему члену, и получите ответ является: 10 0 0 0 0 0 0 1 1 f (a, b, c, d) a bc d = (1, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15). 2 0 0 0 0 1 0 Аналогично, найдите количество минимальных членов, являющихся формой 3 0 0 0 0 1 1 в оставшихся трех функциях. третья функция является и представлена.
Раскрытие скобок дает 8 1 0 0 0 0 0 1 1 Ответ: 9 1 0 0 0 0 1 1 f ( A , B , C , D ) A ( BC D ABCD ABCD ) ABCD (5), 10 1 0 0 1 0 1 0 1 1 То есть функция состоит из единственного минтерма с номером 5. 11 1 0 1 1 1 1 1 1 1 12 1 1 1 1 0 0 1 B , C , D ) AD AC BC = (6, 7, 8, 9, 11, 12, 13, 14, 15).14 1 1 1 1 1 0 1 В некоторых случаях, когда выражение простое, можно использовать только 15 1 1 1 1 1 1 1 1 постоянные преобразования. Это означает, что она может быть выполнена без таблицы истинности. Пример 2: Найти СПНФ функции f ( A , B , C ) A ( B AC BC ).
Решение. Раскройте скобки и преобразуйте выражение: f ( A , B , C ) A ( B AC BC ) = AB ABC = AB ( C C ) ABC = = A BC A B C ABC = (0, 1, 2). Ответ: 0, 1, 2. Пример 3. Найдите СПНФ функции f ( B , C , N ) BCN BCN BCN BCN BCN BCN. Решение. Выражение дано в СПНФ. Поэтому, чтобы найти ответ, просто замените наименьший член на соответствующее число: f ( B , C , N ) BCN BCN BCN BCN BCN BCN (3, 6, 2, 5) (2, 3, 5, 6). Ответ: 2, 3, 5, 6. 3. Применение карт Вейча для минимизации булевых типов 3. 1. Минимизация булевых функций, заданных СДНФ в классе ДНФ Минимизация булевых типов с помощью карт Вейча сводится к визуальному поиску простых следствий, не все возможные, но целые Только те, которые охватывают все единицы и номера карты в целом. Количество символов во всех найденных простых импликациях должно быть минимальным по сравнению с другими типами, представляющими данную булеву функцию. На рисунках 1-3 представлены карты Вейча с тремя, четырьмя и пятью переменными соответственно, где количество минимальных термов записано в полях ячейки и логического аргумента. Эти карты можно использовать для отображения булевых функций, заданных списком минимальных номеров термов. На рисунке 4-33 показан пример минимизации булева выражения A E A A A A B 12 14 6 4 B 25 29 13 9 24 28 12 8 13 15 7 5 27 31 15 B 6 7 3 2 D 11 26 30 14 10 D 4 5 1 0 9 11 3 1 19 23 7 3 18 22 6 2 8 10 2 0 17 21 5 1 16 20 4 0 C C C C C Рисунок 1 . Рис. 2. Форма .3. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 . 4 Рис. 5 Рис. 6 Рис.

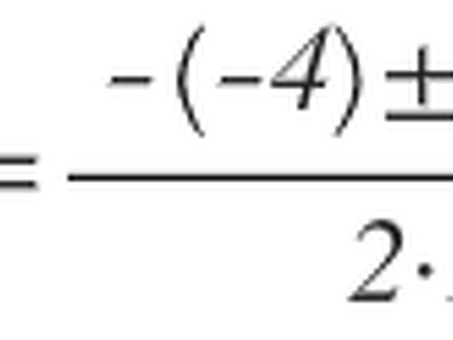




Комментарии