Переписка.
Соответствие G множеств x и y называется тройным объектом: g = (x, k, g), где x - соответствующая область отправления, y - соответствующая область прибытия, а g - соответствующий граф, g ⊆ x × y.
Поле определения поля называется PR 1 G.
Назовите ценовое поле PR 2 G.
Если PR 1 g = x, то соответствие является универсально определенным.
Если NP 2 g = y, то соответствие называется поверхностью.
Соответствие называется функциональным, если граф не содержит пар с одинаковыми первыми и разными вторыми координатами.
Совпадение называется внимательным, если граф не содержит пар с одинаковыми вторыми и разными первыми координатами.
Конгруэнция называется x-t o-to- и везде называется конкретной функцией.
Соответствие называется изображением Х на У, если оно является универсально неполноценным, функциональным и подчиненным.
Матч называется взаимной односторонностью, если он является функциональным и интенсивным.
Соответствие называется биореальным, если оно является универсально определенным, подчиненным, функциональным и влиятельным.
Фотография множества a определенной конгруэнции называется множеством g(b)=
Картиной множества b при определенном соответствии является множество g-1(b)=.
Наборы называются эквивалентными, если между ними можно создать раздел.
Множество называется измеримым, если его касаются все натуральные числа.
Множество называется непрерывным, если оно относится ко всем действительным числам на отрезке [0. 1].
Работа 1. 3. 1
Представьте матч в виде графа.
Выясните, какая из четырех основных характеристик (определение, гипертензия, функция и неприятие) G.
Найдите оригинальные изображения всего набора A и B конкретного матча.
Постройте соответствие между бесконечными множествами, которые имеют тот же набор свойств, что и G.
Постройте соответствие между конечными множествами, которые имеют противоположный набор свойств по отношению к указанному соответствию. Наблюдение. Для данного совпадения и изготовленного совпадения запишите совпадения, определите их тип и отметьте случай организма.
Наблюдение. Для данного соответствия и произведенного соответствия отметьте соответствующие случаи, определите их тип и отметьте случай биекции.
нет x y g a b 1 a, b, c, d, e 1, 2, 3 (a, 2), (b, 3), (c, l), (d, 2), (e, l) e, c 2 , 3 2 a, b, c, d 1, 2, 3, 4 (a, 4), (b, 3), (c, 2), (d, 1) a, b 1. 3 3 a, b, c , d 1, 2, 3, 4, 5 (a, 3), (b, 5) (c, 4), (d, 1) a, c 1. 4 a, b, c, d, e 1, 2 , 3, 4 (d 1), (b, 2), (e, 4), (a, 3) b, c 1. 2 5 a, b, c, d, e 1. 2, 3 (b, 2), ( (c, 1), (e, 3), (a, 3) e, c 3. 1 6 a, b, c, d 1, 2, 3, 4 (a, 2), (b, 2) 3), (c, 1), (a, 4) a, b 1. 2 7 a, b, c, d, e 1, 2, 3, 4, 5 (a, 5), (b, 3), (d, 1), (d, 1), () e, 2) d, e 1. 3 8 a, b, c d 1, 2, 3, 4 (a, 3), (b, 4), (c, 3), (d, 1) a, c 1. 3 9 a , b, c 1, 2, 3 , 4, 5 (a, 2), (b, 1), (c, 5), (a, 3) a, b 3. 4 10 a, b, c 1, 2, c 1, 2, 3 (a, 1), (a, 3), (b, 2), (c, 3) a, c 2. 3 11 a, b, c, d 1, 2, 3, 4, 5 (a, 2) , (c, 1), (d, 5), (c, 3) b, c 1. 2 12 a b, c, d, e 1, 2, 3, 4 (b, 1), (c, 3), (d, 2), (c, 1) a, c 1, 2 13 a, b, c, d 1, 2, 3 (a, 1), (b, 1), (c, 3) , (b, 2) b, d 1. 3 14 a, b, c, d 1, 2, 3, 4 (a, 4), (b, 3), (b, 2), (c, 3) 3), () D, 4) a, b 3. 4 15 a, b, c, d 1, 2, 3, 4 (a, 4), (c, 4), (b, 2) (a, 3) a, b 2, 4 16 a, b, c, d, e 1, 2, 3 (a, 2), (b, 1), (d, 3), (e, 1) a, b 1, 2 17 a, b, c, d 1, 2, 3, 4 (b, 3), (a, 2 ), (c, 2), (d, 1) a, c 1, 4 18 a, b, c, d 1, 2, 3, 4 (a, 3), (c, 2), (d, 1), (c, 4) c, d 2. 3 19 a, b, c 1, 2, 3, 4. 5 (a, 2) (b, 5), (c, 4), (b, 3) a, b 2. 5 20 a, b, c, d 1, 2, 3, 4 (a, 1) (b, 3), (a, 2), (c, 4) a, b 2. 3 21 a, b, c, d 1. 2, 3. 4 (a, d 1. 2) 1), (b, 3), (a, 2), (c, 4) a, b 2. 3 22 a, b, c, d 1, 2, 3 (a, 1), (b, 3), ((b, 3)), (c, 2), (a, 2) a, b 2, 3 23 a, b, c, d 1, 2, 3 4 (a, 3), (b, 4), (c, 1), (d , 2) a, b 1. 4 24 a, b, c 1, 2, 3, 4 (a, 3), (b, 1), (c, 2), (c, 1) a, c 4. 2 25 a, b, c, d, e 1, 2, 3 (c, 2), (d, 1), (a, 3), (b, b 3) a, d 3. 1 26 a, b, c, d 1, 2, 3, 4 (b, 2), (c, 3), (d, 1), (b, 4) b, c 1. 2 27 a, b, c d, e 1, 2, 3, 4, 5 (b (b) , 5), (c, 3), (e, 1), (a, 2) a, e 1. 3 28 a, b, c, d 1, 2, 3, 4 (b, 3), (c, 4 ), (d, 3), (a, 1) b, d 3. 1 29 a, b, c 1, 2, 3, 4. 5 (b, 3), (c, 4), (d, 3), (a , 1) b, d 3. 1 30 a, b, c 1, 2, 3 (b, 1), (b, 3), (c, 2), (a, 3) a, b 2. 3
Примеры решения проблем 1. 3. 1
Представьте соответствие в виде графика (рис. 1. 3. 1, а).
Найдите качества соответствия: a) NPJG - это x. b) NP2G =Y. c) Соответствие совсем не убедительно, потому что соответствие не функционально. d) Соответствие не убедительно, потому что соответствие не функционально. (5) Используйте одинаковые первые и разные вторые координаты. d) Соответствие инъективно, так как граф G не содержит пары одинаковых вторых и разных первых координат.
Найдем образ g (a) и оригинал g-1 (b). g (a) =, a = и⊆g g-1 (b) =, b = и только (d, 4) ⊆g.
Построим соответствие между бесконечными множествами, обладающее тем же набором свойств, что и данное соответствие. Пусть Х=[0,2], У = (-оо,+оо), G = 0>. Покажем, что эта спичка (рис. 1. 3. 1, б) имеет тот же набор свойств, что и эта.
(a) Построенное соответствие не является универсально определенным, так как nptg = [0, l]*x.
(b) Матч не является продуктивным, потому что np2g = [-l, l]*k.
(c) Совпадения не являются функциональными, например, (OD)EC и (0, -1).
(d) Соответствия введены, так как график не содержит пар с различными первой и второй квадратичными координатами.
Построим соответствие между конечными множествами, представим его в виде графа (рис. 1. 3. 1, в) и детализируем его так, чтобы оно было универсально отсутствующим, субъективным, функциональным и бессубъективным.
Покажем, что существует набор свойств, для которых это конкретное свойство необходимо для данного соответствия.
(a) Действительно, это соответствие везде определено, так как np 1 g = x =.
(b) Матч продуктивен, так как np 2 g = = y.
(c) Соответствие функционально, потому что ни одна пара на графике не имеет одинаковых первых и разных вторых координат.
(d) Матч не является двунаправленным, поскольку его граф состоит из двух пар (u, w) и (v, w).
Построенная конгруэнтность является изображением X в Y, потому что она ясна, всеохватна и функциональна везде.
Проблема 1. 3. 2
Для соответствия g = (x, y, g)
Устанавливает набор свойств, принадлежащих данному совпадению.
Постройте соответствие между заполненными наборами, используя свойства, противоположные определенному соответствию, и подробно представьте соответствие в виде графа.
Наблюдение. Обратите внимание на визуальный и биологический случаи.
X Y G 1 многочлен степени 2 от одной переменной с вещественными коэффициентами R (многочлен, его корни) 2 множество кубов на плоскости множество точек на плоскости (окружность, ее центр) 3 (0, + ∞) [-1, 1] ( x, y)|x 2 4 N R (x, ± 1n x) 5 R непрерывная функция на [a, b] 6 университеты вашего города жители вашего города (университет,... кто закончил этот университет) 7 ( 0, + ∞) отрезок прямой (x, отрезок прямой длины x) Фамилии 8 студентов вашей группы (фамилия, количество букв из фамилии) 9 окружности в Z-плоскости (окружность, ее длина) 10 определение функции на [0, 1] R (функция, вертикальные координаты точки ее максимума) 11 R 2 N 12 фамилии студентов вашей группы Русский алфавит буквы (имя, буквы из имени) 13 N студентов вашего университета (n, год рождения человека n) 14 [0 , 1] (x, f(x)), где 15 R R 10 (maxa i ,(a t , a 2 . a 10 )) 1≤i≤10 16 Окружность на плоскости является прямой на плоскости (окружность, касательная к окружности) 17 [P(U)] 3 P(U) ((A, B, C), A⌒B⌒C) 18 [0, 1] R 2 (x,(x, y)|x 2 + y 2 = 1) 19 R функция непрерывна на [0, 1] 20 P(U) [P(U)] 3 21 N (x, y)|x y делится на 3 22 [1, 3] R + (x, y)|(x-2) 2 + ( y- 2) 2 ≤1 23 Пара окружностей на плоскости R 2 (пара окружностей, координаты пересечения этих окружностей) 24 Много книг в университетской библиотеке Z (книга, количество страниц в книге) 25 (- 4, 4) [1, 6] (x, y)|y=|x-2|+1 26 мужчины в вашем городе Женщины в вашем городе (x, y)|x и y состоят в законном браке или были женаты друг на друге 27 [P( U)] 2 P(U) ((A, B) A\B) 28 Политическая партия в вашем городе Жители вашего города ((партия), (которые принадлежат к этой партии) 29 P(U ), где U = N (A,|A|), где A∈P (U) 30 пар прямых в плоскости R (пары прямых, пропасти пересечений прямых)
Пример решения задачи 1. 3. 2
Для X = N, Y - множество непрерывных функций на [a, b], а график G задан как G = .
1 Давайте определим набор свойств, которыми обладает эта коммуникация.
(a) Для каждого натурального числа p мы можем рассмотреть непрерывную функцию f(x) = . Тогда, вычисляя определенный интеграл, получаем: f(x) = f(x) = f(x) = f(x) = f(x) = f(x).
Таким образом, мы видим, что это соответствие очевидно везде.
b) Для некоторых непрерывных функций на [a, b] это соответствие не дифференцируемо, так как определенный интеграл не выражается в терминах натуральных чисел.
c) Покажем, что две разные функции могут иметь одинаковое значение определенного интеграла на рассматриваемом интервале. Для этого можно рассмотреть функции
В случае f (x), как уже установлено, частный интеграл [a, b] по пространству [a, b] равен n. Найдите соответствующий интеграл g (x): n = n.
Это доказывает, что связь, описанная в соглашении о назначении, не работает.
(d) Для каждой функции вводится это соглашение, поскольку конкретное интегрирование в конкретном пространстве является уникальным.
2. построить соответствия между конечными множествами так, чтобы они не были полностью определенными, подчиненными, функциональными или нереспубликанскими.
g
(a) Соответствие G не является универсально отсутствующим, поскольку элемент C в поле отправления не имеет изображений под указанным соответствием.
(b) Совпадение GA является поверхностным, поскольку поле прибытия совпадает с полем цены.
(c) Соответствие GA является функциональным. (c) Соответствие GA является функциональным, поскольку его граф не содержит пар с одинаковыми первыми и разными вторыми координатами.
(d) ГА является небиотопическим, так как на его графике пары (a, 1) и (b, 1) имеют разные начальные и равные вторые координаты, поэтому соответствующий ГА является небиотопическим.
Задание 1. 3. 3
Установить B D Определяет бион между 2A
Тип 18 #512887
Натуральные числа a, b, c и d удовлетворяют условию a > b > c >D.
(a) Для A + B + C + D = 15 и A 2-B 2 + C 2-D 2 = 27 найдите числа a, b, c и d.
(b) a + b + c + d = 19 и a 2-b 2 + c 2-d 2 = 19 может быть.
(c) a + b + c + d = 1000 и a 2-b 2 + c 2-d 2 = 1000.
(a) Условия следующие.
После получения: или
В первом случае неравенства мы находим, каким оно было бы, потому что оба числа и имеют разные обменные курсы.
В последнем случае из неравенства находим, что
(b) Условия следующие.
невозможно, потому что последнее равенство применимо только потому, что мы получаем одинаково.
(c) Равенство имеет место: следовательно, мы получаем четверной материал чисел: кроме того, откуда
Следовательно, A принадлежит пространству (251; 500). Более того, для каждого целого числа A из пространства четыре числа удовлетворяют положению дел. Таким образом, A может иметь значение 248.
Ответ: a) a = 7, b = 5, c = 2, Δ = 1, b) нет, c) 248.
Критерий валидации:.
- Разумное решение для (а).
- Пункт B. Пример.
- Пункт C - оценка, необходимая для оператора управления.
Давайте рассмотрим использование команды IF в примере 3 из работы в этой главе. Мы не будем уделять пристального внимания интерфейсу созданной программы, чтобы читатель мог понять алгоритмы и то, как они написаны на свободном Паскале. .
Задача 3. 1. Дано действительное число. Для функции, график которой изображен на рис. 3. 10, вычислите.
Более подробно, функция, показанная на рис. 3. 10, может быть записана как: x
4, & x \ l e-2, \ x^2, &-2
Чтобы решить эту проблему, создайте алгоритм слов.
Начало алгоритма.
Числовые записи (аргументы функции).
Если значение меньше или равн о-2, перейдите к шагу 4. В противном случае перейдите к шагу 5.
Вычислите значение функции: перейдите к шагу 8.
Если значение равно или больше 1, перейдите к шагу 6. В противном случае перейдите к шагу 7.
Вычислите значение функции: перейдите к шагу 8.
Вычислите значение функции.
Выводит аргументы и значение функции.
Конец алгоритма.
Блок-схема, соответствующая описанному алгоритму, показана на рисунке 3.11. Как видите, блок-схема яснее и проще для понимания, чем словесное описание алгоритма. В будущем блок-схемы будут часто использоваться для объяснения алгоритмов.
Рисунок 3.11. блок-схема алгоритма решения задачи 3.1.
Программа программы в свободном Паскале выглядит следующим образом
var x, y: real; write ( 'x ='); readln (x); if x = 1, y: = 1 else y: = sqr (x); writeln ( 'x =', x: 5:2, 'y =', y: 5:2); end.
Эта программа может быть набрана в текстовом редакторе Geany Text Editor (или Free Pascal) и выполнена.
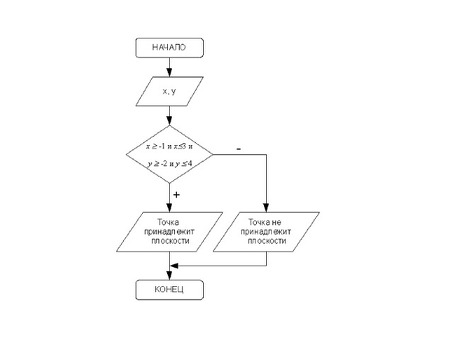
Задача 3. 2. Дано вещественное число. Проверьте, принадлежит ли точка координат заштрихованной части плоскости (рис. 3. 12).
Как показано на рис. 3. 12, эта область является касательной к линии. Таким образом, точка с координатами принадлежит области, если выполняются следующие условия: точка не находится в поле, точка не находится в поле, точка не находится в поле, точка не находится в поле и точка не находится в поле. В противном случае точка находится за пределами поля.
Блок-схема, описывающая алгоритм решения этой задачи, показана на рис. 3. 13.
Рисунок 3. 12. Графическое представление задачи 3. 2.
Рисунок 3. 13. Алгоритм решения задач 3. 2.
Текст программы для задачи 3. 2: (x = -1) и (x = -2).
var x, y : real; begin write ( ’ x= ’ ); readln ( x ); write ( ’ y= ’ ); readln ( y ); if ( x>= -1) и (x = -2) и (y
Работа 3. 3. Создайте программу для решения квадратного уравнения ax^2 + bx + c = 0.
Входные данные: вещественные и - коэффициенты квадратного уравнения.
Рисунок 3. 14. Алгоритм решения квадратного уравнения.
Результат программы: действительные числа и - корни квадратного уравнения - или сообщение о том, что корней нет.
Вспомогательные переменные: фактические переменные, в которых хранится тщательная мощность квадратного уравнения.
Составьте словесный алгоритм для решения этой задачи.
Начало алгоритма.
С обзором числовых значений переменных.
Рассчитайте стоимость различия по типам.
Если нет, продолжите с пункта 6, если нет, продолжите с пункта 5.
Появится сообщение 'No valid roots', и вы перейдете к шагу 8.
Вычисление корней \right)/(2a)" /> и \right)/(2a)" />.
Выведите цену также на экран.
Конец алгоритма.
Блок-схема, соответствующая этому описанию, показана на рис. 3.14.
Текст программы реализация решения квадратного уравнения:.
var a, b, c, d, x1, x2: real; writeln begin ('введите коэффициенты квадратного уравнения'); readln (a, b, c); d: = b*b-4*a*c- d writeln ('нет действительных корней') else begin x1: = (-b+sqrt( d) / 2 / a-x2: = (-b_sqrt (d)) / (2 * a) - writeln ( 'x1 =', x1: 6:3, '-x2 =', x2: 6:3) end.
Задача 3. 4. Создайте программу для нахождения действительных комплексных корней квадратного уравнения.
Входные данные: вещественные и - коэффициенты квадратного уравнения.
Результат программы: действительные числа и - действительные корни квадратного уравнения - или - действительная приятная часть комплексных чисел.
Вспомогательные переменные: фактические переменные, в которых хранится тщательная мощность квадратного уравнения.
Для решения этой проблемы можно выделить следующие шаги
Введение коэффициентов квадратного уравнения.
Расчет дискретной способности по типам.
Проверьте преданность незаметной способности. Вычислите действительные корни, если таковые имеются.
>\text x_2 = \frac>" />
и вывод их на экран. При отрицательном дискриминанте выводится сообщение о том, что действительных корней нет, и вычисляются комплексные корни 4 Комплексные числа записываются в виде , где — действительная часть комплексного числа, — мнимая часть комплексного числа, — мнимая единица " />.
Рисунок 3. 15. Алгоритм решения задачи 3. 4
+i\frac >, \frac-i\frac >." />
У обоих комплексных корней действительные части одинаковые, а мнимые отличаются знаком. Поэтому можно в переменной x1 хранить действительную часть числа , в переменной x2 — модуль мнимой части /(2a)" />Извлеките корни x1+ix2 и x1-ix2.
На рисунке 3. 15 показана блок-схема решения проблемы. Поле 1 предназначено для введения коэффициентов квадратного уравнения. Блок 2 вычисляет ненавязчивую мощность. Блок 3 контролирует знак различия - если различимый отрицательный, то корни комплексные и вычисляются в блоке 4 (действительная часть корня описывается модулем переменной x1, приятная часть переменной x2), выходя в блок 5 (первый корень x1+ix2, второй x1-x2). Если скромная сила положительна, то вычисляются действительные корни уравнения (блоки 6-7) (блок 8).
Текст программы, реализующей проблему:.
var a, b, c, d, x1, x2 : real; begin writeln ( ’Введите_коэффициенты_квадратного_уравнения ’ ); readln ( a, b, c ); d:=b * b-4*a*c; if d x1:=-b /(2 * a ); x2:= sqrt ( abs ( d ) ) / ( 2 * a ); writeln ( ’Комплексные корни уравнения ’, a : 1 : 2, ’ x^2+ ’, b : 1 : 2, ’ x+ ’, c : 1 : 2, ’=0 ’ ); >writeln ( x1 : 1 : 2, '+i * ( ', x2 : 1 : 2, ' ) '), writeln ( x1 : 1 : 2, '- i * ( ', x2 : 1 : 2, ' ) ' ), end else begin x1:=(-b+sqrt ( d ) / 2 / a, x2: =(-b_sqrt ( d ) ) / ( 2 * a )). writeln ( 'Действительные корни уравнения ', a : 1 : 2, ' x^2+ ', b : 1 : 2, ' x+ ', c : 1 : 2, '=0 '). writeln ( 'X1= ', x1 : 1 : 2, ' X2= ', x2 : 1 : 2 ) end.
Задача 3.5. Напишите программу для решения кубического уравнения.
Форма кубического уравнения выглядит следующим образом.
( 3. 1)
Деление на уравнение (3. 1) дает нормальную форму.
(3. 2)
Где В уравнении (3. 2) делается подстановка для получения упрощенного уравнения.
( 3. 3)
, q = \frac - \frac+t." />
Количество значимых корней в упрощенном уравнении (3. 3) зависит от знака дискриминанта упрощенного уравнения третьего порядка (табл. 3. 1).
Таблица 3.1. Количество корней кубического уравнения Дискриминант Количество действительных корней Количество комплексных корней D >0 1 2 D 3 -.
Корни текущего уравнения можно вычислить по формуле Кардано
+\fraci\sqrt\\ y_ & = \frac>-\fraci\sqrt \end" />(3. 4)
]>, v=\sqrt[]>." />
При отрицательной дискретизации уравнение (3. 1) имеет три вещественных корня, которые вычисляются по вспомогательным комплексным числам. Чтобы устранить это, можно использовать следующее уравнение.
\right),\\ y_3&=2\sqrt[3]\cos\left(\frac+\frac \right), \end" />( 3. 5)
>, \cos(\varphi)=\frac." />
Поэтому, если дискриминант кубического уравнения (3. 3) положительный, используйте уравнение (3. 4) для вычисления корней; если отрицательный, используйте уравнение (3. 5).
После вычисления корней уравнения (3. 3) с помощью уравнения (3. 4) или (3. 5)
=y_-\frac, k=1,2,3\ldots" />
Перейдите к корням заданного кубического уравнения (3. 1).
Блок-схема решения кубического уравнения показана на рисунке 1. 3. 16.
Рисунок 3. 16. Алгоритм решения кубического уравнения.
Описание блок-схемы. Коэффициенты кубического уравнения вводятся в блок 1, а коэффициенты нормального и упрощенного уравнений вычисляются в блоках 2 - 3. Поле 4 используется для расчета разрешения. Блок 5 проверяет знак дискриминанта кубического уравнения. Если корни отрицательные, то они вычисляются по уравнению (3. 5) (квадрат 6-7). Если дискриминант положительный, то расчет производится по уравнению (3. 4) (разделы 9 и 10). Поля 8 и 11 используются для отображения результатов на экране.
Текст программы с комментариями приведён ниже5 5 При расчёте величин и в программе предусмотрена проверка значения подкоренного выражения. Если \pm \sqrt > 0" />, то + \sqrt> > 0" />, а - \sqrt> > 0" />. Если \pm \sqrt , то + \sqrt> > 0" />, а - \sqrt> > 0" />. Таким образом, если значение субкорреляционного уравнения равно нулю, оно преобразуется в ноль.
var a, b, c, d, r, s, t, p, q, ro, f i, x1, x2, x3, u, v, h, g : вещественные числа; begin //Вставьте коэффициенты для кубических уравнений. Write ('a='); readln (a); write ('b='); readln (b); write ('c= '); readln ( c ); write ('d='); readln ( d );/ Вычислите коэффициенты нормального уравнения в 3. 2. r :=b/a- s := c /a- t :=d/a- / Вычислите коэффициенты нормального уравнения. 3. 3. p :=(3 * s - r * r ) / 3- q:=2* r * r /27- r * s/3+ t- / Вычисляет дискрет кубического уравнения. d :=( p /3) * sqr ( p/3 ) + sqr ( q / 2 );// Проверяет знак выражения дискриминанта и // переходит к реализации выражения (3. 5). // ветвление в противном случае - Уравнение 3. 4 if d0 then u:=exp (1/3 * ln (-q/2+ sqrt ( d ) ) else i f-q/2+ sqrt ( d ) 0 then v:=exp (1/3 * ln (-q/2- sqrt ( d ) ) els e-q/2- sqrt ( d )
Задача 3.6. Даны коэффициенты α, β и γ билинейного уравнения. Найдите все их истинные корни.
Входные данные: a, b, c . Выходные данные: x1, x2, x3, x4 .
Чтобы решить квадратное уравнение, нужно заменить его квадратным уравнением и решить уравнение.
Опишем алгоритм решения этой задачи (рис. 3. 17).
Введите квадратное уравнение и коэффициенты в (блок 1).
Вычислите дифференциальное уравнение (блок 2).
Если (блок 3), выдать сообщение, что корней нет (блок 4); в противном случае определить корни соответствующего квадратного уравнения (блок 5).
Затем, если (блок 6), он выдает сообщение, что корня нет (блок 7); в противном случае он определяет корень соответствующего квадратного уравнения (блок 8).
Если и (блок 8), то вычисляются четыре корня по формулам , \pm \sqrt" />(блок 9) извлекается корневое значение (блок 10).
Если условия 4) и 5) не выполняются, то необходимо проверить знак . Если 0" /> (блок 11), то вычисляются два корня по формуле " /> (блок 12), иначе (если 0" />) Два корня вычисляются с помощью выражения (блок 13).
Вычисленные значения корней выводятся (блок 14).
Рисунок 3.17. Алгоритм решения квадратных уравнений
Бесплатная программа на языке Паскаль с комментариями Текст:
//Описание переменных: //a,b,c - коэффициенты биквадратного уравнения, //d - дискриминант, //x1,x2,x3,x4 - корни биквадратного уравнения, //y1,y2 - корни квадратного уравнения ay^2+by+c=0. var a, b, c, d, x1, x2, x3, x4, y1, y2 : real; begin //Ввод коэффициентов уравнения. writeln ( ’Введите коэффициенты биквадратного уравнения ’ ); readln ( a, b, c ); //Вычисление дискриминанта. d:=b * b-4*a*c; //Если он отрицателен, if d= 0, else begin //вычисление корней квадратного уравнения. y1:=(-b+sqrt ( d ) ) / 2 / a; y2:=(-b-sqrt ( d ) ) / ( 2 * a ); //Если оба корня квадратного уравнения = 0, else if ( y1>=0) and ( y2>=0) then begin //вычисление четырех корней биквадратного уравнения. x1:= sqrt ( y1 ); x2:=-x1; x3:= sqrt ( y2 ); x4:=-sqrt ( y2 ); //Вывод корней биквадратного уравнения на экран. writeln ( ’X1= ’, x1 : 6 : 3, ’ X2= ’, x2 : 6 : 3 ); writeln ( ’X3= ’, x3 : 6 : 3, ’ X4= ’, x4 : 6 : 3 ); end //Если не выполнились оба условия // 1. y1=0 И y2>=0, //то проверяем условие y1>=0 else if ( y1>=0) then //Если оно истинно begin x1:= sqrt ( y1 ); x2:=-x1; writeln ( ’X1= ’, x1 : 6 : 3, ’ X2= ’, x2 : 6 : 3 ); end else //Если условие y1>Если =0 ложно, начинаем x1:= sqrt ( y2 ); x2:=-x1; writeln ( 'X1= ', x1 : 6 : 3, ' X2= ', x2 : 6 : 3 ); end end end. Объясните номера деталей Kingston.
Узнайте, как читать каталожные номера модулей памяти Kingston®, включая модули Kingston серий FURY™, Server Premier™ ValueRAM®, HyperX®, DDR5, DDR4, DDR3, DDR2 и DDR. Это поможет вам определить модули памяти на основе их технических характеристик.
Kingston FURY™ DDR5
Следующая информация призвана помочь вам идентифицировать модули памяти Kingston FURY на основе технических характеристик.
Номер детали: KF556C38BBE2AK2-32
KF = Линия продуктов
KF = Kingston FURY
5 = Технология
5 - DDR5
56 = Скорость (МТ/сек * )
52 - 5200
56 - 5600
60 - 6000
64 - 6400
68 - 6800
72 - 7200
C = Тип устройства
C - UDIMM (без разделения, без ECC)
S-SODIMM (без изоляции, без ECC)
38 = Задержка CAS
3 2-CL32
3 6-CL36
3 8-CL38
4 0-CL40
B - Зверь
I-Effect
Р - вероотступник
B = тепловая энергия
B- ?
S - серебро
E = Типовой профиль
Не указано - Intel XMP / Plug and Play
E-AMD Expo
Не указано - версия 1ᴙ
2-Версия 2ᴙ
3 - Версия 3ᴙ
Не указано - Заднее освещение RGB Нет
A-RGB
K2 = общее количество + количество модулей
Не указано - единичное устройство
K2- Комплект из 2 единиц
K4- Комплект из 4 единиц
16 = общая вместимость
8-8 ГБ
16-16 ГБ
32-32 ГБ
64-64 ГБ
128-32 ГБ
Kingston Server Premier DDR5
Следующая информация предназначена для идентификации модулей памяти Kingston Server Premier на основе технических характеристик.
Номер компонента: KSM48R40BD4TMP-64HMR
KSM = серия изделий
KS M-Kingston Server Premier
48 = Номинальная скорость (MT/S*)
48-4800
52 - 5200
56 - 5600
r = Тип устройства
e-ec4udimm (x72)
l-ec8 lrdimm (x80)
P-EC4 RDIMM (X72)
r-ec8 rdimm (x80)
T-EC4 SODIMM (X72)
40B = задержка CAS
40B-CL40-39-39
42-CL42-42-42
46B-CL46-45-45
S-Grade
D-2 Материк
Q-четверной выкуп
4 = Тип барабана
I-Ренесас
К - Рихтек
M-Editorial
П - Парламентарий
T-ti
M = Втулка СПД
I-Ренесас
M-Editorial
R - Rambus
P = датчик температуры
I-Ренесас
M-Editorial
П - Парламентарий
R - Rambus
64 = Вместимость
16-16 ГБ
32-32 ГБ
64-64 ГБ
128-128 ГБ
H = Производитель DRAM
H - SK Hynix
M-Micron
S - Samsung
M = версия с барабаном для чипсов
A - умереть
C-C Die
умирать
m-m умереть
r = Регистрация
I-Ренесас
M-Editorial
R - Rambus
Kingston Valiram DDR5
Номер компонента: KVR48U40BS8K2-32X
KVR = Заказ продукции
KV R-Kingston Valeeram
48 = Номинальная скорость (MT/S*)
48-4800
52 - 5200
56 - 5600
60 - 6000
u = тип устройства
u-dimm (без разделения, без ECC)
S-s o-dimm (без разделения, без ECC)
40B = задержка CAS
40 B-CL40
42 B-CL42
46 B-CL46
S-Peer-to-Peer
D-EMERITUS Вход
8 = Тип памяти DRAM
8-x8
6-x16
K2 = общее количество + количество модулей
Не указано - единичное устройство
K2- Комплект из 2 единиц
K4 - комплект из 4 единиц
32 = общая вместимость
8-8 ГБ
16-16 ГБ
32-32 ГБ
64-64 ГБ
128-128 ГБ
256-256 ГБ
x = регулировка
Не определено - стандартный пакет
BK - большая упаковка
Kingston Fury™DDR4/DDR3 Номер компонента Номер декодирования
Следующая информация призвана помочь вам идентифицировать модули памяти Kingston FURY на основе технических характеристик.
Номер детали: KF432C16BB1AK4/64
KF = Линия продуктов
KF = Kingston FURY
4 = Технология
3 - DDR3
4 - DDR4
32 = Скорость (МТ/сек * )
16 - 1600 (1. 5V)
16Л - 1600 (1. 35В)
18 - 1866 (1. 5V)
18L - 1866 (1. 35V)
26 - 2666
32 - 3200
36 - 3600
37 - 3733
40 - 4000
42 - 4266
46 - 4600
48 - 4800
50 - 5000
51 - 5133
53 - 5333
C = Тип устройства
C - UDIMM (без разделения, без ECC)
S - SODIMM (без разделения, без ECC)
16 = Задержка CAS
9 - CL9
10 - CL10
11 - CL11
13 - CL13
15 - CL15
16 - CL16
17 - CL17
18 - CL18
19 - CL19
20 - CL20
B - Зверь
R - Renegade
I - импликация
B = тепловая энергия
Не указано - синий
B - черный
R - красный
W - белый
Не указано - 1
1 - модуль 16 ГБ с элементами 1Gx8 (8 Гбит)
2 - 2-е издание
3 - 3-й пересмотр
4 - 4-й пересмотр
Не указано - Заднее освещение RGB Нет
A - RGB-подсветка
K4 = общее количество + количество модулей
Пустой - отдельный блок
K2 - комплект из 2 единиц
K4- Комплект из 4 единиц
K8 - комплект из 8 единиц
64 = общая вместимость
4 - 4 ГБ
8 - 8 ГБ
16 - 16 ГБ
32 - 32 ГБ
64 - 64 ГБ
128 - 128 ГБ
256 ГБ - 256 ГБ
Kingston Server Premier DDR4
(PC4-2400, PC4-2666, PC4-2933, PC4-3200)
Номер детали: KSM26RD4L/32HAI
KSM = серия изделий
KSM - Kingston Server Premier
26 = Скорость (MT/s*)
24 - 2400
26 - 2666
29 - 2933
32 - 3200
R = Тип устройства
E - неизолированный модуль DIMM (ECC)
R - Registered DIMM
L - DIMM с пониженной нагрузкой
SE - неизолированный SO-DIMM (ECC)
S - односпальная кровать
D - Двойной
Q - площадь
4 = Тип DRAM
L = профиль печатной платы
L - Очень низкопрофильный модуль DIMM
32 = общая вместимость
8 - 8 ГБ
16 - 16 ГБ
32 - 32 ГБ
64 - 64 ГБ
128 - 128 ГБ
256 - 256 ГБ
H = Производитель DRAM
H - SK Hynix
M-Micron
A = Новая версия микросхемы DRAM
A - Чип
B - B Чип
E - E Чип
I = Создатель реестра
I-IDT
M-Editorial
R - Rambus
Kingston ValueRAM DDR4
(PC4-2133, PC4-2400, PC4-2666, PC4-2933, PC4-3200)
Номер детали: KVR21LR15D8LK2/4HBI
KVR = Заказ продукции
KVR = Kingston ValueRAM
21 = Скорость (MT/s * )
21 - 2133
24 - 2400
26 - 2666
29 - 2933
32 - 3200
L = Низкое напряжение
Не указано - 1. 2 В
r = Тип устройства
E - небуферизованный модуль DIMM с датчиком температуры (с ECC)
L - DIMM с уменьшенной нагрузкой (LRDIMM)
N - неизолированный модуль DIMM (без ECC)
R - регистр DIMM с температурно-чувствительной четностью адреса/команды
S - SODIMM, неизолированный (неECC)
15 = Задержка CAS
15 - CL15
19 - CL19
22 - CL22
S-Grade
D-2 Материк
Q-четверной выкуп
O - Восьмикратный пробег
8 = Тип памяти DRAM
4 - x4
8-x8
6-x16
L = Профиль
Не указано - любая высота
Высота - 31. 25 мм
L - 18. 75 мм (VLP)
K2 = общее количество + количество модулей
Не указано - единичное устройство
K2 - комплект из 2 единиц
K3 - комплект из 3 единиц
4 = Общая мощность
4 - 4 ГБ
8-8 ГБ
16-16 ГБ
32-32 ГБ
H = Производитель DRAM
H - SK Hynix
К - Кингстон
М - Микрон
S - Samsung
B - издание
I = Intel Certified
I - Intel Certified
Описание номера детали HyperX®
Следующая информация предназначена для идентификации модулей памяти Kingston HyperX на основе технических характеристик.
Номер детали: HX429C15PB3AK4/32
HX = Линия продукции
HX = HyperX (предыдущее устройство)
4 = Технология
3 - DDR3
4 - DDR4
29 = Скорость (МТ/сек * )
13 - 1333
16 - 1600
18 - 1866
21 - 2133
24 - 2400
26 - 2666
28 - 2800
29 - 2933
30 - 3000
32 - 3200
33 - 3333
34 - 3466
36 - 3600
37 - 3733
40 - 4000
41 - 4133
42 - 4266
46 - 4600
48 - 4800
50 - 5000
51 - 5133
53 - 5333
C = DIMM Тип памяти
C - UDIMM (небуферизованный неECC)
S - SODIMM (неECC без буферизации)
15 = Задержка CAS
9 - CL9
10 - CL10
11 - CL11
12 - CL12
13 - CL13
14 - CL14
15 - CL15
16 - CL16
17 - CL17
18 - CL18
19 - CL19
20 - CL20
F - Память
B - Зверь
S - дикий
P - Хищник
I - импликация
B = тепловая энергия
Синий - не указано
B - черный
R - красный
W - белый
2 - 2-е издание
3 - 3-й пересмотр
4 - 4-е издание
Не указано - RGB Без подсветки
A - RGB-подсветка
K4 = множество + количество модулей в множестве
Не указано - единичное устройство
K2 - комплект из 2 единиц
K4- Комплект из 4 единиц
K8 - комплект из 8 единиц
32 = общая вместимость
4 - 4 ГБ
8 - 8 ГБ
16 - 16 ГБ
32 - 32 ГБ
64 - 64 ГБ
128 - 128 ГБ
256 ГБ - 256 ГБ
DDR3
(PC3-8500, PC3-10600, PC3-12800)
Описание номера детали ValueRAM
например, Новая машина: KVR 16 R11 D4/8 Старая машина: KVR 1600 D3 D4 R11 S/8G
Новая система нумерации применяется к продукции, произведенной после 1 мая 2012 года.
Номер детали: KVR16LR11D8LK2/4HB
KVR = Kingston ValueRAM
КВР: Кингстон Валерам.
16 = скорость (мт/с *)
16: 1600
13: 1333
10: 1066
L = Низкое напряжение
Нет названия: 1. 5V
L: 1. 35V
U: 1. 25 В
R = Тип устройства
E: без изоляции (ECC)
N: dimm без разделения (не ECC)
R: регистрация яркости
L: диммирование с пониженной нагрузкой (lrdimm)
S: so-dimm
11 = задержка (CAS)
11: задержка (CAS)
S: один
D: Тандем
Q: 4 раза рейтинг
8 = Тип барабана
4: Барабанный чип x4
8: Барабанный наконечник x8
L = Профиль
L: 18,75 мм (VLP)
H: 30 мм
K2 = общее количество + количество единиц
K2: Комплект из 2 единиц
K3: Комплект из трех единиц
K4: Комплект из четырех единиц
4 = Хранение
4: 4 ГБ
8: 8 ГБ
12: 12 ГБ
16: 16 ГБ
24: 24 ГБ
32: 32 ГБ
48: 48 ГБ
64: 64 ГБ
H = DRAM MFGR/ Сертифицированный
H: Hynix
В: Предпочтительный
I: сертифицировано Intel
B: Версия для микросхем
B: Кристаллическая версия
DDR3 & DDR2
DDR3 (PC3-8500, PC3-10600) & DDR2 (PC2-3200, PC2-4200, PC2-5300, PC2-6400)
Номер компонента: KVR1066D3LD8R7SLK2/46HB
KVR = Kingston ValueRAM
КВР: Кингстон Валерам.
1066 = Скорость (мт/с *)
1066 = Скорость
D3 = Технология
D2: DDR2
D3: DDR3
L = Низкое напряжение
Нет названия: 1. 5V
L: 1. 35V
U: 1. 25 В
D = Технология
S: один
D: Тандем
Q: 4 раза рейтинг
4: Барабанный чип x4
8: Барабанный наконечник x8
R = Тип устройства
P: Регистратор управления участком (только для модулей с регистратором)
E: без изоляции (ECC)
F: FB Dimm.
M: Mini-Dimm
N: dimm без разделения (не ECC)
R: DIMM с адресом/устройством связи Регистрация
S: so-dimm
U: micro-dimm
7 = задержка (CAS)
7: задержка (CAS)
S = тепловой датчик
Без знака: без термодатчика
S: с датчиком температуры
L = Профиль
Безымянный: без имени
L: 18,75 мм (VLP)
H: 30 мм
K2 = общее количество + количество единиц
Безымянный: индивидуальное единство
K2: Комплект из 2 единиц
K3: Комплект из трех единиц
4G = сохранить
4G = сохранить (гб)
H = DRAM MFGR
H: DRAM MFGR
B: вопрос
ddr.
(PC2100, PC2700, PC3200)
Номер компонента: KVR400X72RC3AK2/1G
KVR = Kingston ValueRAM
КВР: Кингстон Валерам.
400 = Скорость (мт/с *)
X72 = X72 ECC
X72: X72 ECC
r = Регистрация
R: Регистр.
C3 = задержка (CAS)
C3: Задержка (CAS)
A = DDR400 3-3-3
A: DDR400 3-3-3
K2 = общее количество + количество единиц
K2: Комплект из 2 единиц
1 г = хранение
1 г = объем памяти (ГБ)
Задержка (синхронизация)
Следующая информация поможет вам понять различные параметры, которые можно настроить при задании оптимальных таймингов памяти в BIOS родительской карты. Обратите внимание, что эти настройки могут отличаться у разных марок и моделей материнских плат, а также у разных версий прошивки BIOS.
Пример.
TRA/TRD/TRS
Задержка CAS: задержка между активацией и считыванием одной строки.
Задержка RAS-CAS или задержка колонки RAS: активация строки
Защита задержки RAS (TRP/TRCP): деактивирует строку
Задержка активной строки или задержка активной RAS или время считывания (TRD/TRD/TRS): количество тактов между строками активации/деактивации.
Заявление о раскрытии информации об ответственности. Все продукты Kingston были протестированы в соответствии с опубликованными спецификациями. Некоторые конфигурации систем или материнских плат могут не работать на опубликованных скоростях или с опубликованными временными настройками модулей памяти Kingston. Kingston рекомендует пользователям не пытаться перегружать компьютер сверх опубликованных скоростей; чрезмерная дата процессора или системы может повредить компоненты компьютера.
* Для получения дополнительной информации о мегалитрах в секунду, MT/s означает количество мегаломов (миллионов передач) в секунду и представляет собой фактическую скорость передачи данных памяти DDR (двойные данные) SDRAM Блок памяти DDR SDRAM посылает нарастание и спад за каждый тактовый цикл (1 Гц). Пример: DDR4-3200 (PC4-3200) Тактовая частота: 1600 МГц Скорость передачи данных: 3200 MT/s Зональный диапазон: 25, 600 MB/s (25. 6 GB/s)





Комментарии