7.3.1. Примеры для закрепления формул сокращенного умножения , a b 2 b 2.
5620.00 ₽
Февраль 15, 2023
16
1. умножения
Чтобы возвести сумму в квадрат, к квадрату суммы первого и второго уравнения можно добавить удвоенное произведение, умноженное на два.
На практике:.
a & plus- b 2 = a & plus- bbo a & plus- b = a a & plus- a b & plus-b вычесть a & plus B ⋅ b = a 2 & plus ab & plus ba & plus b 2 = a 2 & plus 2 ab & плюс b 2.
z & Plus; 5 2 = z 2 & Plus; 2⋅z⋅5 & Plus; 5 2 = z 2 & Plus; 10 z & Plus; 25.
2. разность: A-B 2 = A 2-2 AB & Plus; B 2.
Чтобы возвести разность в квадрат, можно отнять от суммы квадратов первого и второго уравнений удвоенное произведение.
На практике:.
a-b 2 = a-b b-a -b =a⋅a & Plus - a a t-b - b-b⋅ a-b b-b Желаемый = a 2-a b-ba & Plu s-b 2 = A 2-Ab 2 & Plu s-b 2. 7. 3. 1 Примеры для закрепления формул сокращенного умножения
(1) Квадрат суммы двух уравнений равен квадрату первого уравнения плюс квадрат второго уравнения плюс удвоенное значение первого уравнения плюс квадрат второго уравнения.
(a + b) 2 = a 2 + 2ab + b 2
(a) (x + 2y)2 = x 2 + 2-x -2y + (2y)2 = x 2 + 4xy + 4y 2
(b) (2k + 3n)2 = (2k)2 + 2- 2 k-3n + (3n)2 = 4k 2 + 12kn + 9n 2
(2) Квадрат разности между двумя уравнениями равен квадрату первого уравнения, а квадрат второго уравнения равен квадрату первого уравнения, умноженному на квадрат второго уравнения.
( A-B)2 = A 2-2AB+B 2
(a) (2 a-c) 2 = (2a) 2-2- 2 a-c + c 2 = 4a 2-4ak + c 2
(b) (3 a-5b) 2 = (3a) 2-2- 3 a-5b + (5b) 2 = 9a 2-30ab + 25b 2
(3) Разность квадратов двух уравнений равна произведению разностей самих уравнений.
a 2-b 2 = ( a-b)(a+b)
(a) 9x 2-16y 2 = (3x) 2 - (4y) 2 = (3 x-4y) (3x + 4y)
(b) (6 k-5n) (6k + 5n) = (6k)2-(5n)2 = 36k 2-25n 2
(4) Куб суммы двух уравнений равен кубу первого уравнения плюс тройное произведение первого уравнения на второе уравнение плюс тройное произведение первого уравнения на второе уравнение плюс куб второго уравнения плюс квадрат второго уравнения.
(a +b)3 = a 3 +3a 2 b +3ab 2 +b 3
(a) (M + 2N)3 = M 3 + 3-M 2-2N + 3-M-(2N)2 + (2N)3 = M 3 + 6M 2 N + 12MN 2 + 8N 3
(b) (3x + 2y)3 = (3x)3 + 3 - (3x) 2-2y + 3- 3x- (2y)2 + (2y)3 = 27x 3 + 54x 2 y + 36xy 2 + 8y 3
(5) Куб разности двух уравнений равен кубу первого уравнения минус тройное произведение первого уравнения на второе уравнение минус тройное произведение первого уравнения на квадрат второго уравнения.
( a-b)3 = a 3-3a 2 b+3ab 2-b 3
(a) (2 x-y)3 = (2x) 3-3-(2x) 2-y + 3- 2 x-y 2-y 3 = 8x 3-12x 2 y + 6xy 2-y 3
(b) ( x-3n)3 = x 3-3- x 2- 3n + 3- x - (3n)2- (3n)3 = x 3-9x 2 n + 27xn 2-27n 3
(6) Сумма кубов двух уравнений равна произведению суммы самих уравнений на неполный квадрат уравнения.
a 3 + b 3 = (a + b) (a 2 - ab + b 2)
(a) 125 + 8x 3 = 5 3 + (2x)3 = (5 + 2x) (5 2-5-2x + (2x)2) = (5 + 2x) (25-10x + 4x 2)
(b) (1 + 3m) (1-3m + 9m 2) = 1 3 + (3m)3 = 1 + 27m 3
(7) Разность кубов двух уравнений равна произведению разностей самих уравнений и равна неполному квадрату их суммы.
a 3-b 3 = ( a-b) (a 2 + ab + b 2)
(a) 64c 3-8 = (4c) 3-2 3 = (4 c-2) (4c) 2 + 4 c-2 + 2 2) = (4 c-2) (16c 2 + 8c + 4)
(b) (3 a-5b) (9a 2 + 15ab + 25b 2) = (3a) 3 - (5b) 3 = 27a 3-125b 3
Дорогой друг, карта сайта поможет вам найти нужную тему. a b 2 b 2
Решение.
a) (b - 2) (b + 2) (b 2 + 4) = (b 2-4) (b 2 + 4) = b 4-16; b) ( 3-y) (3 + y) (9 + y 2) = ( 9-y 2) (9 + y 2) = 8 1-y 4; c) (a 2 + 1) (a + 1) (a - 1) = (a 2 + 1) (a 2-1) = a 4-1; d) (c 4 + 1) (c 2 + 1) -1) = (c 4 + 1) (c 4-1) = c 8-1; e) ( x-3) 2 (x + 3) 2 = (( x-3) (( x-3) (x + 3)) 2 = (x 2-9) 2 = x 4-18x 2 + 81; f) (y + 4) 2 ( y-4) 2 = ((y + 4) ( y-4)) 2 = (y 2-16) 2 = y 4-32y 2 + 256; g) ( a-5) 2 (5 + a) 2 = (( a-5) (5 + a)) 2 = ((a 2-25) 2 = a 4-50a 2 + 625; h) (c + 4) 2 ( 4-c) 2 = ((c + 4) ( 4-c)) 2 = (1 6-c 2) 2 = 256-32c 2 + c 4.
Похожие проблемы:.
Постройте четыре различные конструкции:.
(a) Сечение A1B1 симметричное, сечение AB относительно точки C
(b) Сечение A2C2 симметрично сечению AC и AB.
(c) Секция A3B3, образованная параллельным сдвигом секции AB на вектор AC; и
(d) Секция A4C4. Она образуется при непрерывном повороте влево на 90° отрезка ABC вокруг точки b.
Запишите координаты точек A1, B1, A2, C2, A3, B3, A4, C4. Задача 11880 Найдите значение b+(2a-b^2)/b.
Если a = 49 и b = 10, найдите значение выражения b+(2a-b^2)/b
8-9-й Математика 20382
Решение.
Вопрос с решением (6)
Запрос: VK186283680.
Откуда берется b²?
Приведение суммы к общему знаменателю: (b*b/b)+((2a-b^2)/b) = (b^2+2a-b^2)/b
Вопрос: u21387154208.
Откуда взялось B^2?
Уменьшение общего знаменателя и умножаем в на в
Вопрос: u80832398.
(b/1) + ((2a-b^2)/b) = общий знаменатель B = (b*b/b) + ((2a-b^2)/b) = (b²/b) + ((2a-b²)/b = записать в дробной строке = (b²+2ab²)/b = 2a/b Значение формулы ((a^2-b^2)/2ab): ( 1/a- 1 /b) a = 1. 1 и b = 2. 9 корпус.
Очень трудно рассчитать, непосредственно подставляя числа в эту формулу. Было бы обидно ошибиться в цифрах на экзамене.
В целом, к концу седьмого класса все ученики должны уметь упрощать такие уравнения. В этом и заключается идея. Однако в реальности это удается лишь 15%.
Что произойдет, если вы упростите это уравнение? Позвольте мне коротко объяснить.
1) Двоичное число в числителе первой дроби сокращается. по формуле сокращенного умножения Разность квадратов": a 2-b 2 = (a-b)(a+b).
2) Дробь в скобках приводится к общему знаменателю ab.
3) Когда дробь делится на дробь, знак деления равен умножения вторая фракция обратная.
4) Все возможное сокращается (выделено синим и зеленым цветом). При сокращении противоположных выражений, таких как (α-β) и (β-α), перед дробью ставится знак минус.
5) Подставьте число первой дроби и посчитайте.

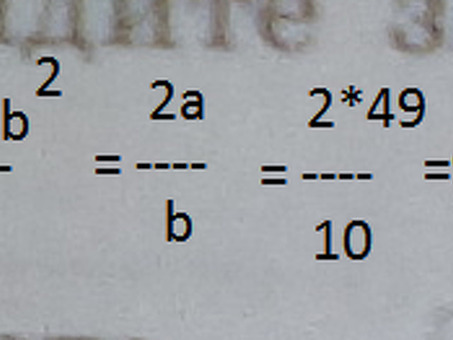




Комментарии