При выполнении измерений или расчетов важно понимать понятия соответствующей погрешности и абсолютной погрешности. Эти два термина используются для количественной оценки точности и погрешности измерений или расчетов.
Абсолютная погрешность представляет собой разницу между измеренной или рассчитанной ценой и фактической или допустимой ценой. Это мера того, насколько измерение или расчеты далеки от желаемого значения. Абсолютная погрешность часто выражается в единицах измерения или расчета.
Сопутствующая погрешность, с другой стороны, представляет собой причину абсолютной погрешности относительно фактического или допустимого значения. Она представляет собой более нормированную меру точности, учитывающую размер измеряемой или рассчитываемой величины. Сопутствующие погрешности часто выражаются в процентах или десятичных числах.
Как абсолютные, так и сопутствующие погрешности дают важную информацию о точности и достоверности измерений или расчетов. Абсолютная погрешность показывает, насколько измерение или расчет отклонились от желаемого значения, а сопутствующая погрешность позволяет сравнивать точность различных измерений или расчетов, независимо от их размера.
Понимание и количественная оценка этих двух понятий необходимы в самых разных дисциплинах, включая науку, технику и статистику. Оценка и минимизация как абсолютной, так и относительной погрешности позволяет повысить точность и надежность измерений и расчетов.
Понимание релевантных погрешностей.
Относительная погрешность - это величина, используемая в математике и естественных науках для количественной оценки точности вычисленных значений по сравнению с фактическими. Она дает возможность выразить разницу между расчетными и точными ценами в относительном смысле.
Для понимания сопутствующих погрешностей важно сначала разобраться с понятием абсолютной погрешности. Конечная ошибка - это разница между расчетной и фактической ценой. Однако конечные погрешности не дают стандартного способа сравнения точности различных расчетов или измерений.
Соответствующие погрешности, напротив, нормализуют конечную погрешность путем деления ее на фактическое значение. Это позволяет проводить более содержательные сравнения между различными расчетами или измерениями. Соответствующая погрешность выражается в доводах или процентах и однозначно указывает на точность оценки или измерения.
Например, рассмотрим ситуацию, когда вы пытаетесь оценить вес объекта. Его масса равна 10 кг, но фактическая масса составляет 9,5 кг. Итоговая погрешность в этом случае составляет 10 кг - 9,5 кг = 0,5 кг. Однако если выразить погрешность, то она составит 0,5 кг / 9,5 кг ≈ 0,0526 или 5,26%.
Используя соответствующую погрешность, можно увидеть, что расчетная стоимость примерно на 5,26% больше фактической. Это позволяет принимать более обоснованные решения или соответствующим образом корректировать расчеты. Сопутствующие ошибки особенно полезны при работе с большими числами или при сравнении величин разного размера.
Определение релевантной погрешности
Соответствующая погрешность - это мера точности или погрешности вычисленного или измеренного значения, выраженная в виде причины или процента по отношению к фактическому или допустимому значению. Она сравнивает разницу между рассчитанной или измеренной ценой и фактической или допустимой ценой и обеспечивает способ количественной оценки размера ошибки по отношению к размеру фактического или допустимого значения. Сопутствующая погрешность обычно используется в научных и механических расчетах и экспериментах для оценки качества полученных данных.
Математически сопутствующая погрешность может быть рассчитана путем деления сопутствующей погрешности на фактическое или допустимое значение, которое затем может быть выражено в процентах путем умножения на 100. Видами соответствующей погрешности являются.
(| рассчитанная/измеренная цена - истинная/допустимая цена|/истинная/допустимая цена) * 100%.
Например, предположим, что ученый измеряет длину объекта как 25 см, а известно, что фактическая длина объекта составляет 24 см. Итоговая погрешность в этом случае составляет 1 см. Для расчета соответствующей погрешности необходимо разделить конечную погрешность на фактическую длину и умножить на 100.
Сопутствующая погрешность = (1 см / 24 см) * 100% ≈ 4. 17%.
Это означает, что относительная погрешность измеренной длины составляет примерно 4,17% по отношению к фактической длине. Соответствующая погрешность дает возможность измерить, насколько близка измеренная величина к фактической с учетом размера фактической величины. Ученые и инженеры могут оценивать качество и надежность расчетов и измерений и принимать решения, основываясь на точности и корректности данных.
Расчет абсолютной погрешности
При измерении и анализе точности экспериментальных или расчетных величин важную роль играет понятие абсолютной погрешности. Абсолютная погрешность - это мера того, насколько измеренная или рассчитанная величина далека от действительного или истинного значения.
Для расчета абсолютной погрешности необходимо из действительного или истинного значения вычесть измеренное или рассчитанное значение (называемое также приближенным). Полученное значение и есть абсолютная погрешность - величина разности между двумя значениями, независимо от того, больше или меньше эти два значения.
Например, если действительное значение равно 10, а измеренное или рассчитанное значение равно 9, то абсолютная погрешность равна 1. Если фактическое значение равно 15, а измеренное или рассчитанное - 17, то абсолютная погрешность также равна 2. В обоих случаях абсолютная погрешность - это величина разности, независимо от того, больше или меньше истинное значение измеряемой величины.
Когда сообщается об абсолютной погрешности, она обычно выражается положительным значением. Это связано с тем, что абсолютная погрешность представляет собой величину разности и не имеет конкретного направления. Поэтому принято игнорировать знак минус и выражать абсолютную погрешность в виде положительной величины.
При сравнении абсолютных погрешностей различных измерений или вычислений важно отметить, что меньшая абсолютная погрешность свидетельствует о большей точности. Это означает, что значения с меньшими абсолютными погрешностями ближе к истинному или действительному значению, чем значения с большими абсолютными погрешностями. Поэтому абсолютная погрешность может служить полезным инструментом для оценки точности измерений и вычислений в различных областях, таких как физика, инженерное дело и экспериментальные науки.
Как рассчитать абсолютную погрешность
Для расчета абсолютной погрешности необходимы две величины: измеренное значение и истинное или допустимое значение. Абсолютная погрешность - это разность между измеренным и действительным значением.
Предположим, вы измеряете длину объекта и получаете значение 10 см, а фактическая длина составляет 9,5 см. Для расчета абсолютной погрешности необходимо из измеренного значения вычесть истинное.
Абсолютная погрешность = измеренное значение - истинное значение
В данном случае абсолютная погрешность составляет
Абсолютная погрешность = 10 см - 9,5 см = 0,5 см.
Абсолютная погрешность - это величина разности между измеренным и действительным значением. Она показывает, насколько далеко измеренное значение от действительного.
Важно отметить, что абсолютная погрешность всегда положительна, так как представляет собой абсолютное значение разности. Это означает, что абсолютная погрешность всегда будет положительной, независимо от того, больше или меньше измеренное значение по сравнению с действительным.
Вычисление абсолютной погрешности позволяет оценить точность измерения и определить, насколько оно близко к истинному значению. Это полезный инструмент в различных научных и математических дисциплинах, где важна точность измерений.

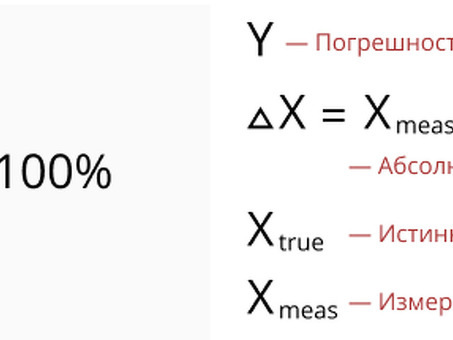


Комментарии